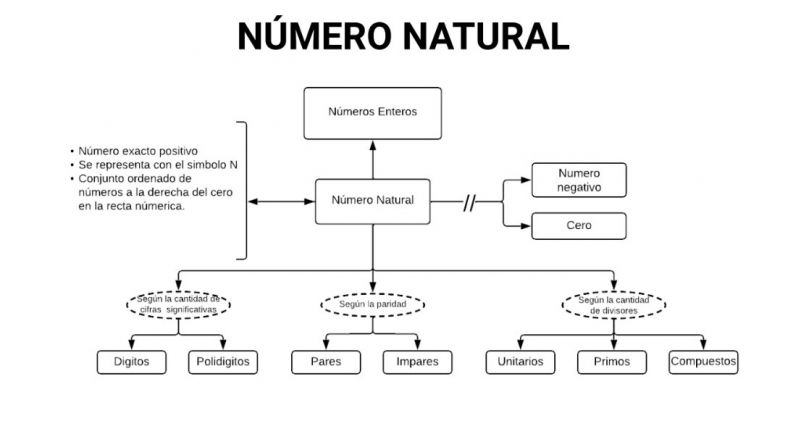
Mentefacto Número Natural
Paquete proposicional
Supraordinada
P1: Todo número natural es número entero.
Isoordinadas
P2.1:Todo número natural es número exacto positivo.
P2.2: Todo número natural se representa con el símbolo N.
P2.3: Todo número natural es un conjunto ordenado a la derecha del cero en la recta numérica.
Exclusiones
P3.1: Ningún número natural es número negativo.
P3.2: Ningún número natural es cero.
Infraordinadas
P4.1.1: Algunos números naturales según su cantidad de cifras son dígitos.
P4.1.2: Algunos números naturales según su cantidad de cifras son polidígitos.
P4.2.1: Algunos números naturales según la paridad son pares.
P.4.2.2: Algunos números naturales según la paridad son impares.
P.4.3.1: Algún número natural según la cantidad de factores son unitarios.
P.4.3.2: Algún número natural según la cantidad de factores son primos.
P.4.3.3: Algún número natural según la cantidad de factores son compuestos.
- Mentefactos Proposicionales
P1: Todo número natural es número entero.
P2.1:Todo número natural es número exacto positivo.
P2.2: Todo número natural se representa con el símbolo N.
P2.3: Todo número natural es un conjunto ordenado a la derecha del cero en la recta numérica.
P3.1: Ningún número natural es número negativo.
P3.2: Ningún número natural es cero.
P4.1.1: Algunos números naturales según su cantidad de cifras son dígitos.
P4.1.2: Algunos números naturales según su cantidad de cifras son polidígitos.
P4.2.1: Algunos números naturales según la paridad son pares.
P.4.2.2: Algunos números naturales según la paridad son impares.
P.4.3.1: Algún número natural según la cantidad de factores son unitarios.
P.4.3.2: Algún número natural según la cantidad de factores son primos.
P.4.3.3: Algún número natural según la cantidad de factores son compuestos.
Análisis proposicional
P1: Todo número natural es número entero.
Porque el número entero es aquel que se representa con la letra z. No tiene una parte decimal dentro de su estructura y contiene a los números negativos, el cero y a la totalidad de los números naturales que son infinitos y si le sumamos al uno obtendremos otro número natural. Estos no son fracciones, no tienen decimales ni tienen una unidad imaginaria, a menudo tienen un número sucesor, están en la parte derecha de la recta numérica y pueden sumarse, restarse, multiplicarse o dividirse tal y como los números enteros.
Ejemplos: Z= {...,-3,-2,-1, 0, 1, 2, 3….}
P2.1: Todo número natural es número exacto positivo.
Porque los números exactos positivos son números mayores que cero, son los números que se puede utilizar para contar y que no es necesario poner un símbolo que exprese que es positivo como en el número negativo, es decir, son los números naturales, pero expresados de otra forma y los números negativos son números menores que cero y les antecede el signo negativo.
Ejemplos: 1, 2, 3, 4, 5
P2.2: Todo número natural se representa con el símbolo N.
Porque debido a la importancia de este conjunto de números se creó un símbolo especial para identificarlo, como lo es la letra N para representar el conjunto de los números naturales, además con la ayuda de este símbolo se puede mostrar la formulación del número par y el impar que son (2N) y (2N +-1) respectivamente.
Ejemplos:
2(5)=10 → Número Par
2(6)+1=13 → Número Impar
N→7
P2.3: Todo número natural es un conjunto ordenado a la derecha del cero en la recta numérica.
Porque en la recta numérica se representan a los números enteros que son los números naturales o números positivos, los números negativos y al cero, los números naturales son mayores hacia la derecha, mientras que los negativos son cada vez más pequeño a medida que se avanza a la izquierda, ambos se extienden hacia el infinito y el cero es el punto medio entre los números negativos y los positivos.
Ejemplos: … -4, -3, -2, -1, 0, 1, 2, 3, 4 …
P3.1. Ningún número natural es número negativo.
Argumentación:
Porque aunque los números negativos, el cero y los números naturales o números positivos forman parte de los números enteros, difieren en sus características, como se puede evidenciar en que los números naturales son aquellos que se representan a la derecha del 0 en una recta numérica, en cambio, los números negativos son todos aquellos números que se representan a la izquierda del cero y se expresan con un signo menos para que no se confundan con los números naturales.
Ejemplos:
Positivos: 4,5,6,7,8
Negativos: -8,-7,-6,-5,-4
P.3.2. Ningún número natural es cero.
Porque el cero es el que separa a los números positivos o números naturales y los números negativos en la recta numérica, es decir que es el punto medio que marca la división entre los números positivos y negativos, por lo que se puede decir que el cero no pertenece a los números naturales, así como no pertenecen a los números negativos, sino que los tres forman el conjunto de los números enteros.
Ejemplos: -3 -2 -1 0 1 2 3
P4.1.1. Algunos números naturales según su cantidad de cifras significativas son dígitos.
Porque los números naturales no tienen una parte decimal y son números positivos, se pueden clasificar según su cantidad de cifras significativas, que son el número de dígitos en un valor y se pueden dividir en polidígitos y dígitos, que son los diez símbolos que usamos en nuestro sistema de numeración para representar las cantidades.
Ejemplos:1,2,3,4,5,6,7,8,9
P4.1.2. Algunos números naturales según su cantidad de cifras significativas son polidígitos.
Argumentación:
Porque los números naturales no tienen una parte decimal y son números positivos, se pueden clasificar según su cantidad de cifras significativas, que son el número de dígitos en un valor y se pueden dividir en dígitos y polidígitos que son aquellos que presentan más de una cifra numérica. Son aquellos que tienen más de un dígito, de dos hasta infinitos.
Ejemplos: 24,360, 54, 7823
P4.2.1. Algunos números naturales según la paridad son pares.
Porque un número natural es aquel que no tiene parte decimal y se puede dividir según su paridad, que se refiere al atributo de un número de ser impar o par, un número es par cuando se obtiene al multiplicar dos por cualquier número natural, es por ello que se llega a la conclusión de que los números pares son los que terminan en 0, 2, 4, 6, 8 por lo que pueden ser infinitos, pero raras veces van a tener una parte decimal, además que su fórmula es 2N.
Ejemplos: 2, 14, 36, 58
P4.2.2. Algunos números naturales según la paridad son impares.
Porque un número natural es aquel que no tiene parte decimal y se puede dividir según su paridad, que se refiere al atributo de un número de ser par o impar, que son los que no son pares, es decir, son aquellos cuya cifra de las unidades no es cero ni un número par y siempre ocurrirá que al restar la unidad a un número par se obtiene un número impar, por lo que pueden ser infinitos, pero raras veces van a tener una parte decimal, además que su fórmula es 2N-+1.
Ejemplos: 23, 45, 981.
P4.3.1. Algún número natural según la cantidad de divisores son unitarios.
Porque los números naturales son números enteros, es decir que son aquellos que no tienen parte decimal y se pueden dividir según la cantidad de divisores en primos, compuesto y unitario, que es aquel que solamente tiene un divisor, solamente existe un caso y es el número uno, el cual a menudo va a dar como resultado un número que no tiene parte decimal.
Ejemplos: 1
P4.3.2. Algún número natural según la cantidad de divisores son primos.
Porque los números naturales son números enteros, es decir que son aquellos que no tienen parte decimal y se pueden dividir según la cantidad de divisores en unitario, compuesto y primos, que son los que solo son divisibles entre ellos mismos y el uno, es decir, que es aquel que solo tiene dos divisores y si intentamos dividirlo por cualquier otro número el resultado no va a ser un número entero, y por lo tanto, no va a ser un número natural.
Ejemplos: 2, 3, 5, 7
P4.3.3. Algún número natural según la cantidad de divisores son compuestos.
Argumentación:
Porque los números naturales son números enteros, es decir, que son aquellos que no tienen parte decimal y se pueden dividir según la cantidad de divisores en unitario, primos y compuestos, que son los que son divisibles entre ellos, el uno y cualquier otro número natural, es decir, que tienen más de dos divisores, además del uno y de sí mismo y no tiene una parte decimal. Estos números pueden ser expresados como un producto de números primos que es único para cada número.
Ejemplos: 4, 6, 8, 9, 10, 12, 14
Referencias
Math for All. “Los Números Naturales - QUE SÓN Y PROPIEDADES 🤓.” Www.youtube.com, 2022, www.youtube.com/watch?v=KI8l1NOB-9k. Accessed 22 Apr. 2023.
Ascencio, Rebeca. “Números Negativos Y Positivos, ¿Cómo Entenderlos Y Cómo Hacer Las Operaciones Básicas Con Ellos?” IMPULSO MATEMÁTICO, 20 Mar. 2019, impulsomatematico.com/2019/03/20/numeros-negativos-y-positivos-como-entenderlos-y-como-hacer-las-operaciones-basicas-con-ellos/. Accessed 22 Apr. 2023.
Diego. “Cuáles Son Los Números Naturales ?? - Características Y Propiedades.” Www.youtube.com, 2020, www.youtube.com/watch?v=Fswg2NNg0qo. Accessed 22 Apr. 2023.
Equipo editorial. “Números Naturales - Concepto, Usos, Características Y Ejemplos.” Concepto, 13 June 2022, concepto.de/numeros-naturales/.
Rivas, Oscar . “Los Números Naturales | PDF | Decimal | Número Natural.” Scribd, es.scribd.com/document/482105914/LOS-NUMEROS-NATURALES#. Accessed 22 Apr. 2023.
tiempo, Claudia RiveraGraduada en Matemáticas Aplica su experiencia con niños de Altas Capacidades para desarrollar contenido en Smartick Es apasionada de las matemáticas y tiene la firme convicción de que todos podríamos serlo Actriz de teatro empedernida y gran aficionada a la fotografía Si consigue algo de, and Observa Las Estrellas. “Números Primos Y Compuestos: Qué Son + Ejemplos.” Smartick, 11 Sept. 2012, www.smartick.es/blog/matematicas/numeros-enteros/numeros-primos-y-numeros-compuestos/. Accessed 22 Apr. 2023.