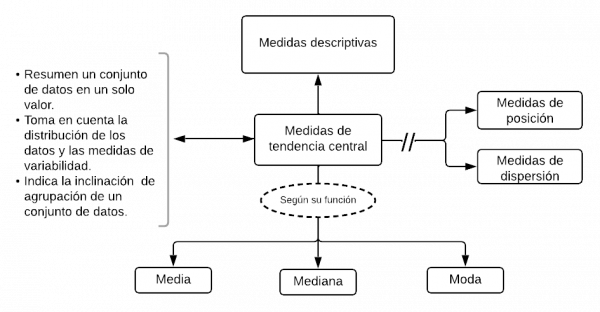
Mentefacto Medidas De Tendencia Central
Paquete Proposicional
Supraordinada
P1: Toda medida de tendencia central es medida descriptiva.
Isoordinadas
P2.1: Toda medida de tendencia central resume un conjunto de datos en un solo valor.
P2.2: Toda medida de tendencia central toma en cuenta la distribución de los datos y las medidas de variabilidad.
P2.3: Toda medida de tendencia central indica la inclinación de agrupación de un conjunto de datos.
Exclusiones
P3.1: Ninguna medida de tendencia central es medida de posición.
P3.2: Ninguna medida de tendencia central es medida de dispersión.
Infraordinadas
P4.1: Alguna medida de tendencia central según su función es media.
P4.2: Alguna medida de tendencia central según su función es mediana.
P4.3: Alguna medida de tendencia central según su función es moda.
- Mentefactos Proposicionales
P1: Toda medida de tendencia central es medida descriptiva.
P2.1: Toda medida de tendencia central resume un conjunto de datos en un solo valor.
P2.2: Toda medida de tendencia central toma en cuenta la distribución de los datos y las medidas de variabilidad.
P2.3: Toda medida de tendencia central indica la inclinación de agrupación de un conjunto de datos.
P3.1: Ninguna medida de tendencia central es medida de posición.
P3.2: Ninguna medida de tendencia central es medida de dispersión.
P4.1: Alguna medida de tendencia central según su función es media.
P4.2: Alguna medida de tendencia central según su función es mediana.
P4.3: Alguna medida de tendencia central según su función es moda.
Argumentaciones
P1: Toda medida de tendencia central es medida descriptiva.
Las medidas descriptivas son valores que resumen la información contenida en un conjunto de datos. Esta puede calcularse a partir de los datos de una muestra o población y se clasifica en medidas de dispersión, medidas de posición, medidas de forma y medidas de tendencia central, las cuales dan como resultado medidas estadísticas que resumen en un solo valor a un conjunto de datos.
Ejemplo: Medidas de tendencia central, medidas de dispersión, medidas de posición.
P2.1: Toda medida de tendencia central indica la inclinación de agrupación de un conjunto de datos.
Son medidas estadísticas que nos dan un centro de distribución de frecuencias, alrededor de los cuales tienden a agruparse todos los datos, por lo que son representativos de todos los datos originales. Las principales medidas de tendencia central son la media, mediana y moda.
Ejemplo: Media, mediana y moda.
P2.2: Toda medida de tendencia central toma en cuenta la distribución de los datos y las medidas de variabilidad.
Ya que la calidad de las medidas de tendencia central está asociada intrínsecamente con la “concentración” de la información.
P2.3: Toda medida de tendencia central indica la inclinación de agrupación de un conjunto de datos.
Una medida de tendencia central, como la media, la mediana o la moda, es una medida estadística que representa el centro o valor típico de un conjunto de datos. Indican la inclinación o agrupación de los datos en torno al valor central. La media es la suma de todos los valores del conjunto de datos dividida por el número de valores, mientras que la mediana es el valor medio del conjunto de datos cuando está ordenado.
P3.1: Ninguna medida de tendencia central es medida de posición.
También llamaba medida de ubicación, es un valor que permite dividir un conjunto de datos en partes porcentuales iguales y se utiliza para clasificar las observaciones en una población o muestra. Las medidas de ubicación más frecuentes son cuartiles, deciles y percentiles.
Ejemplo: Cuartiles, deciles y percentiles.
P3.2: Ninguna medida de tendencia central es medida de dispersión.
Las medidas de dispersión son una herramienta importante en estadística, ya que se utilizan para mostrar la variabilidad de las distribuciones y para indicar hasta qué punto los datos individuales están separados de sus centros, las medidas de tendencia central más utilizadas son: media, mediana y moda. La varianza, por otro lado, mide qué tan dispersos están los valores de una variable. En otras palabras, el propósito de las medidas de dispersión es estimar el grado de dispersión de los datos.
Ejemplo: Varianza, desviación estándar.
P4.1: Alguna medida de tendencia central según su función es media.
Argumentación: La media aritmética se obtiene del cociente entre la suma de todos los datos y el número de datos sumados, es decir, el promedio de todos los valores provenientes de una muestra o población, por lo tanto su fórmula es: Media aritmética=X1+X2+X3...+Xnn . Esta es la media de tendencia central más común, ya que se usa para datos numéricos y distribuciones simétricas, es decir, sin ningún tipo de sesgo, y es sensible a los valores absolutos.
P4.2: Alguna medida de tendencia central según su función es mediana.
Porque la mediana es el valor estadístico que ocupa la posición central en un conjunto de datos. Además, parte el conjunto de datos en dos, es decir, deja la misma cantidad de datos a ambos lados, cuando los datos están ordenados por magnitud, de menor a mayor. Se caracteriza por tener operaciones sencillas para calcular su valor, además este no depende de las variables, pero sí del orden. En caso de tener una cantidad par de datos, habrá dos datos centrales, entonces se debe sacar un promedio de estos y así obtener la mediana. La mediana se emplea para datos ordinales o para datos numéricos con distribución sesgada, porque no es sensible a la variación de los extremos.
Ejemplo: En el conjunto de datos (2,4,5,6,7,9,11), la mediana es 6.
P4.3: Alguna medida de tendencia central según su función es moda.
Porque la moda se define como el valor variable más repetitivo, dentro de un conjunto de datos, que se obtienen de una muestra o población. Estos valores se pueden presentar en variables cualitativas y cuantitativas.
Ejemplo: En el conjunto (3,6,8,7,5,5,7,4,5) la moda es 5, ya que es el dato que más se repite.
Referencias
- “Medidas de Tendencia Central.” Probabilidad Y Estadística, 27 May 2022, www.probabilidadyestadistica.net/medidas-de-tendencia-central/.
- Buitrago, Lina . “Medidas de Tendencia Central Y de Localización.” Rstudio-Pubs-Static.s3.Amazonaws.com, 2020, rstudio-pubs-static.s3.amazonaws.com/657085_7fc690937804488f991b0243a621b8da.html#:~:text=Las%20medidas%20de%20localizaci%C3%B3n%20o. Accessed 22 Apr. 2023.
- Ortega, Cristina. “¿Qué Es La Media, La Mediana Y La Moda?” QuestionPro, 9 Dec. 2018, www.questionpro.com/blog/es/la-media-la-mediana-y-la-moda/#:~:text=Al%20hablar%20de%20medidas%20de. Accessed 22 Apr. 2023.
- Ruiz , Luis . Material Didáctico de Estadística.
- Sepúlveda, Fabio . “RPubs - Documento.” Rpubs.com, 25 Aug. 2020, rpubs.com/FabioSepulveda/medidas_descriptivas#:~:text=Las%20medidas%20descriptivas%20son%20valores.