Mentefacto Conceptual Conjunto
Mentefacto Conceptual
Paquete proposicional
Supraordinada
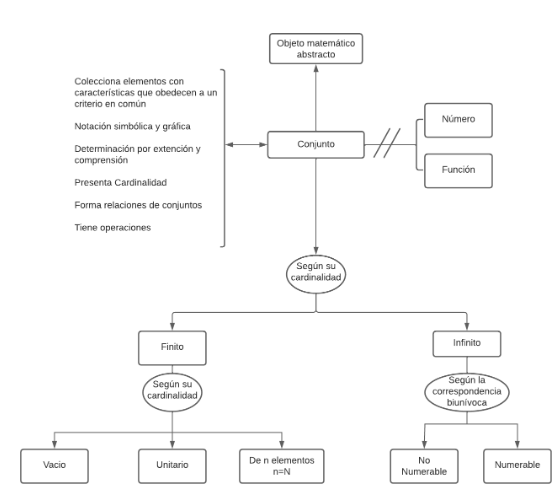
P.1: Todo conjunto es objeto matemático abstracto
Isoordinadas
P.2.1: Todo conjunto colecciona elementos con características obedientes a un criterio común
P.2.2: Todo conjunto posee una notación simbólica y gráfica
P.2.3.1: Algunos conjuntos tienen determinación por extensión
P.2.3.2: Algunos conjuntos tienen determinación por comprensión
P.2.4: Todo conjunto presenta cardinalidad
P.2.5: Los conjunto forman relaciones de conjuntos
P.2.6: Los conjuntos tienen operaciones
Exclusiones
P.3.1: Ningún conjunto es número
P.3.2: Ningún conjunto es función
Infraordinadas
P.4.1: Algún conjunto según su cardinalidad es conjunto finito
P.4.1.1: Algún conjunto finito según su cardinalidad es conjunto vacío
P.4.1.2: Algún conjunto finito según su cardinalidad es conjunto unitario
P.4.1.3: Algún conjunto finito según su cardinalidad es conjunto de N elementos
P.4.2: Algún conjunto según su cardinalidad es conjunto infinito
P.4.2.1: Algún conjunto infinito según la correspondencia biunívoca entre elementos es conjunto infinito no numerable
P.4.2.2: Algún conjunto infinito según la correspondencia biunívoca entre elementos es conjunto infinito numerable
- Mentefactos proposicionales
P.1: Todo conjunto es objeto matemático abstracto
P.2.1: Todo conjunto es una colección elementos con características obedientes a un criterio común.
P.2.2: Todo conjunto posee una notación simbólica y gráfica
P.2.3.1: Algunos conjuntos tienen determinación por extensión
P.2.3.2: Algunos conjuntos tienen determinación por comprensión
P.2.4: Todo conjunto presenta cardinalidad
P.2.5: Los conjunto forman relaciones de conjuntos
P.2.6: Los conjuntos son objetos operables.
P.3.1: Ningún conjunto es número
P.3.2: Ningún conjunto es función
P.4.1: Algún conjunto según su cardinalidad es conjunto finito
P.4.1.1: Algún conjunto finito según su cardinalidad es conjunto vacío
P.4.1.2: Algún conjunto finito según su cardinalidad es conjunto unitario
P.4.1.3: Algún conjunto finito según su cardinalidad es conjunto de n elemento
P.4.2: Algún conjunto según su cardinalidad es conjunto infinito
P.4.2.1: Algún conjunto infinito según la correspondencia biunívoca entre elementos es conjunto infinito no numerable
P.4.2.2: Algún conjunto infinito según la correspondencia biunívoca entre elementos es conjunto infinito numerabl
Argumentaciones
P.1: Todo conjunto es objeto matemático abstracto
Una razón por la cual todo conjunto es considerado un objeto matemático abstracto es porque, en matemáticas, los conjuntos se definen únicamente en términos de sus propiedades lógicas y relaciones con otros objetos matemáticos, independientemente de su existencia física o concreta en el mundo real. Es decir, un conjunto es una entidad abstracta que representa una colección de objetos matemáticos que comparten ciertas características comunes. Esta abstracción permite a los matemáticos trabajar con conjuntos de manera más flexible y general, lo que a su vez les permite modelar y analizar una amplia gama de situaciones matemáticas y físicas. Además, los conjuntos son la base de la teoría de conjuntos, una rama fundamental de las matemáticas modernas. Esta teoría proporciona el lenguaje y la estructura formal necesaria para describir y analizar una amplia variedad de conceptos matemáticos, como los números, las funciones, las relaciones y los mismos conjuntos.
P.2.1: Todo conjunto colecciona elementos con características obedientes a un criterio común
La definición de conjunto implica la agrupación de objetos que comparten alguna propiedad o característica en común. En otras palabras, un conjunto es una colección de objetos que cumple con un criterio específico que los distingue de otros objetos. Por ejemplo, si consideramos el conjunto de números pares, podemos identificar cada elemento del conjunto como aquel número que se puede expresar como el doble de otro número entero. En este caso, la propiedad común que comparten los elementos del conjunto es ser números pares, lo que los distingue de otros números que no cumplen con esta propiedad. Esta idea de agrupar elementos que cumplen con un criterio común es fundamental en la teoría de conjuntos y se utiliza para modelar y analizar una amplia variedad de conceptos matemáticos y físicos. Además, la capacidad de identificar y agrupar elementos según sus propiedades comunes es esencial en la resolución de problemas matemáticos y científicos en general.
P.2.2: Todo conjunto posee una notación simbólica y gráfica
Los conjuntos en matemáticas se definen como colecciones de objetos que comparten una propiedad en común, y se utilizan para modelar y analizar una amplia variedad de conceptos. Toda colección de objetos que cumpla con cierto criterio puede ser considerada un conjunto. Es importante contar con una notación simbólica y gráfica para representar conjuntos, ya que permite describirlos de forma precisa y concisa, y visualizar sus propiedades y relaciones con otros conjuntos. La notación simbólica generalmente consiste en un nombre o letra que representa el conjunto, seguida de teclas que encierran los elementos del conjunto. La notación gráfica, como el diagrama de Venn, representa los conjuntos como regiones en un plano o espacio.
P.2.3.1: Algunos conjuntos tienen determinación por extensión
Algunos conjuntos pueden ser definidos por extensión, lo que implica que sus elementos son especificados limpiamente al enumerarlos o listarlos. Esto es útil para conjuntos finitos o cuyos elementos son fácilmente identificables o enumerables. La determinación por extensión permite identificar los elementos de manera clara y precisa, pero no es adecuada para conjuntos infinitos o sus elementos no son fácilmente enumerables. En estos casos se utiliza la determinación por comprensión.
P.2.3.2: Algunos conjuntos tienen determinación por comprensión
Algunos conjuntos tienen determinación por comprensión, lo que significa que se definen en función de una propiedad o criterio común que cumplen sus elementos. Esta forma de definición es útil para conjuntos con una cantidad infinita de elementos o cuyos elementos no son fácilmente enumerables. La determinación por comprensión permite definir conjuntos en términos de sus propiedades o características, lo que facilita su estudio y análisis.
P.2.4: Todo conjunto presenta cardinalidad
Todo conjunto presenta cardinalidad porque esta propiedad nos permite determinar el número de elementos que contiene el conjunto. La cardinalidad de un conjunto se define como el número de elementos que lo conforman, y se representa mediante el símbolo |A|, donde A es el conjunto. La cardinalidad es una propiedad fundamental de los conjuntos, ya que nos permite realizar comparaciones y operaciones entre conjuntos de diferentes tamaños. Por ejemplo, si tenemos dos conjuntos A y B, podemos comparar su tamaño y determinar si son iguales (si tienen la misma cardinalidad) o si uno es más grande que el otro (si tienen distinta cardinalidad). Además, la cardinalidad nos permite definir conjuntos finitos e infinitos. Un conjunto se considera finito si su cardinalidad es un número natural (por ejemplo, el conjunto de días de la semana tiene una cardinalidad de 7), mientras que un conjunto se considera infinito si su cardinalidad es mayor que cualquier número natural (por ejemplo, el conjunto de números naturales es infinito).
P.2.5: Los conjunto forman relaciones de conjuntos
Los conjuntos forman relaciones de conjuntos debido a que las relaciones entre los elementos de un conjunto y los elementos de otro conjunto pueden ser representados mediante una relación binaria, es decir, una relación que se establece entre dos conjuntos. Esta relación binaria puede ser de diferentes tipos, como la inclusión, la intersección, la unión, la diferencia, la igualdad y la disyunción, entre otras. Por ejemplo, si tenemos dos conjuntos A y B, podemos establecer la relación de inclusión entre ellos, lo que significa que todos los elementos de A están también en B. De manera similar, podemos establecer la relación de convergencia, que se refiere a los elementos que ambos conjuntos tienen en común. La relación de unión, por otro lado, se refiere a la combinación de elementos de ambos conjuntos.
P.2.6: Los conjuntos tienen operaciones
Los conjuntos tienen operaciones porque permiten manipular los elementos que los conforman y obtener nuevos conjuntos. Las operaciones, como la unión, intersección y diferencia, entre otras, tienen definiciones y propiedades específicas que permiten combinar o filtrar elementos de conjuntos para obtener conjuntos resultantes con características particulares. Estas son operaciones útiles en diversos contextos y situaciones para realizar cálculos, comparaciones y análisis de conjuntos.
P.3.1: Ningún conjunto es número
Los conjuntos no son números porque son una colección de objetos o elementos que pueden ser de diferentes tipos, no obstante números. Aunque los conjuntos pueden incluir números, los conjuntos en sí mismos no son números, sino una colección de objetos que se agrupan bajo ciertas condiciones o propiedades. Los conjuntos tienen sus propias y definiciones que son diferentes a las propiedades y definición de los números, por lo que son conceptos distintos que se utilizan en diferentes contextos y situaciones y no pueden ser intercambiados.
P.3.2: Ningún conjunto es función
Debido a que un conjunto es una colección de elementos. Los elementos pueden ser cualquier objeto matemático, como números, letras, figuras geométricas, otros conjuntos, entre otros. Un conjunto se denota por llaves que encierran los elementos, separados por comas, mientras que una función es una relación entre dos conjuntos, donde cada elemento del primer conjunto se relaciona con exactamente un elemento del segundo conjunto. La función toma como entrada un valor del primer conjunto, llamado el dominio, y produce como salida un valor del segundo conjunto, llamado el rango.
P.4.1: Algún conjunto según su cardinalidad es conjunto finito
Debido a que hay conjuntos que tienen una cantidad finita de elementos y, por lo tanto, son finitos en términos de cardinalidad. El cardinal de un conjunto se define como la cantidad de elementos que tiene. Si un conjunto tiene una cantidad finita de elementos, entonces su cardinalidad es un número natural finito, lo que implica que el conjunto es finito. Por lo tanto, es cierto que existe algún conjunto cuya cardinalidad es finita y, por lo tanto, es finito como conjunto.
P.4.1.1: Algún conjunto finito según su cardinalidad es conjunto vacío
Porque Un conjunto finito es aquel que tiene una cantidad finita de elementos, mientras que el conjunto vacío no tiene elementos en absoluto, lo que lo convierte en un caso especial de conjunto finito. Aunque el conjunto vacío no contiene elementos, su cantidad de elementos es cero, lo que lo hace finito. Es importante destacar que el conjunto vacío es distinto al conjunto infinito, ya que este último tiene una cantidad infinita de elementos, normalmente se confunden los conceptos de conjunto vacío y conjunto infinito porque ambos no tienen un límite superior. Sin embargo, el conjunto vacío es el único conjunto finito que no tiene elementos, mientras que el conjunto infinito tiene una cantidad infinita de elementos.
P.4.1.2: Algún conjunto finito según su cardinalidad es conjunto unitario
Porque un conjunto finito es aquel que tiene una cantidad finita de elementos, mientras que un conjunto unitario es aquel que tiene exactamente un elemento. Si un conjunto finito tiene una cardinalidad de uno, entonces ese conjunto es unitario, por lo tanto, cualquier conjunto finito que tenga exactamente un elemento es un conjunto unitario. Por ejemplo, el conjunto {5} es un conjunto unitario, ya que tiene una cardinalidad de uno. En resumen, la proposición establece la relación entre conjuntos finitos y unitarios, demostrando que algunos conjuntos finitos pueden ser unitarios si tienen una cantidad exacta de un solo elemento
P.4.1.3: Algún conjunto finito según su cardinalidad es conjunto de N elementos
Ya que un conjunto finito es aquel que tiene un número finito de elementos. Si un conjunto tiene una cantidad específica y fija de elementos, como ocurre en los conjuntos con n número de elementos, entonces es un conjunto finito, como por ejemplo, si tenemos el conjunto {1, 2, 3}, podemos decir que es un conjunto con 3 elementos y, por lo tanto, es un conjunto finito. Si tenemos el conjunto {a, b, c, d, e}, podemos decir que es un conjunto con 5 elementos y, por lo tanto, es un conjunto finito, por lo que podemos decir que los conjuntos con n número de elementos son finitos, ya que un conjunto es finito si y sólo si tiene un número finito de elementos, y los conjuntos con n número de elementos tienen una cantidad específica y fija de elementos.
P.4.2: Algún conjunto según su cardinalidad es conjunto infinito
Porque un conjunto es infinito si su cardinalidad es mayor que la de los números naturales, es decir, si no puede ser contado de manera finita. Esto significa que no existe una correspondencia uno a uno entre los elementos del conjunto y los números naturales. Un ejemplo clásico de conjunto infinito es el conjunto de números naturales, pero también existen otros, como el conjunto de números enteros, el conjunto de números racionales o el conjunto de todos los números reales. La noción de infinitud es importante en matemáticas porque ha llevado al desarrollo de herramientas y teoremas que permiten el estudio de objetos infinitos, como la teoría de conjuntos, el análisis matemático y la teoría de números.
P.4.2.1: Algún conjunto infinito según la correspondencia biunívoca entre elementos es conjunto infinito no numerable
Ya que el conjunto infinito no numerable es aquel que no puede ser colocado en correspondencia uno a uno con los números naturales. Georg Cantor demostró que existen conjuntos más grandes que el conjunto de los números naturales utilizando la técnica de diagonalización. Un ejemplo de conjunto infinito no numerable es el conjunto de números reales. La idea de infinitud no numerable es importante en matemáticas, ya que llevó al desarrollo de la teoría de conjuntos y ha tenido importantes aplicaciones en análisis matemático.
P.4.2.2: Algún conjunto infinito según la correspondencia biunívoca entre elementos es conjunto infinito numerable
Porque un conjunto infinito numerable es aquel que se puede colocar en correspondencia uno a uno con los números naturales. El conjunto de los números enteros es un ejemplo de conjunto infinito numerable, junto con otros conjuntos como los números pares, los números impares, las fracciones con denominador igual a 1 y las potencias de 2. Por otro lado, existen conjuntos infinitos no numerables, como el conjunto de los números reales. La noción de cardinalidad de un conjunto es importante en la teoría de conjuntos y el estudio de los diferentes tipos de infinitos ha llevado a importantes desarrollos matemáticos.
Referencias
- Halmos, P. R. (1960). Naive set theory. Van Nostrand.
- Jech, T. (2003). Set theory (3rd millennium ed.). Springer.
- Kunen, K. (2011). Set theory: An introduction to independence proofs (Studies in Logic and the Foundations of Mathematics). North-Holland.
- Enderton, H. B. (2001). A mathematical introduction to logic (2nd ed.). Academic Press. Suppes, P. (1972). Axiomatic set theory. Dover Publications.