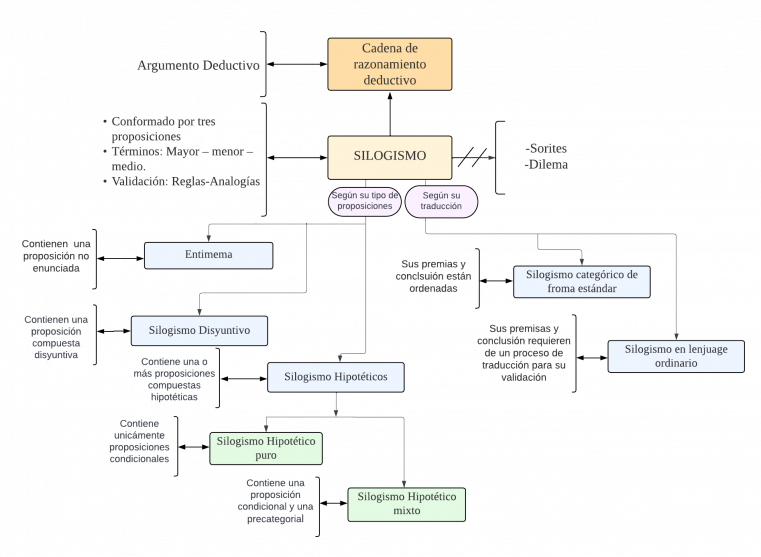
MENTEFACTO SILOGISMO
Paquete Proposicional
Supraordinada
P1. Todo silogismo es Cadena de razonamiento deductivo
Isoordinadas
P2.1 Todo silogismo es un argumento conformado por tres proposiciones.
P2.2 Todo silogismo es argumento que tiene tres términos.
P2.3 Todo silogismo es argumento que se puede validar con reglas y analogías.
Exclusiones
P3.1 Ningún silogismo es Sorites
P3.2 Ningún silogismo es Dilema
Infraordinadas
P4.1 Algún silogismo según su tipo de premisas es Entimema.
P4.2 Algún silogismo según su tipo de premisas es silogismo disyuntivo.
P4.3 Algún silogismo según su tipo de premisas es silogismo hipotético.
P4.3.1 Algún silogismo hipotético es silogismo hipotético puro.
P4.3.2 Algún silogismo hipotético es silogismo hipotético mixto.
P4.4.1 Algún silogismo según su traducción es silogismo categórico en forma estándar
P4.4.2 Algún silogismo según su traducción es silogismo en lenguaje ordinario
- Mentefactos Proposicionales
P1. Todo silogismo es Cadena de razonamiento deductivo
P2.1 Todo silogismo es un argumento conformado por tres proposiciones.
P2.2 Todo silogismo es argumento que tiene tres términos.
P2.3 Todo silogismo es argumento que se puede validar con reglas y analogías.
P3.1 Ningún silogismo es Sorites
P3.2 Ningún silogismo es Dilema
P4.1 Algún silogismo según su tipo de premisas es Entimema.
P4.2 Algún silogismo según su tipo de premisas es silogismo disyuntivo.
P4.3 Algún silogismo según su tipo de premisas es silogismo hipotético.
P4.3.1 Algún silogismo hipotético es silogismo hipotético puro.
P4.3.2 Algún silogismo hipotético es silogismo hipotético mixto.
P4.4.1 Algún silogismo según su traducción es silogismo categórico en forma estándar
P4.4.2 Algún silogismo según su traducción es silogismo en lenguaje ordinario
Argumentaciones
P1. Todo silogismo es una cadena de razonamiento deductivo.
Un argumento deductivo es aquel cuyas premisas pretenden proporcionar bases concluyentes para la verdad de su conclusión y un silogismo es cualquier argumento deductivo en el que la conclusión infiere de dos premisas.
P2.1 Todo silogismo es un argumento conformado por tres proposiciones.
Las proposiciones de este argumento son aristotélicas o también llamadas categóricas que se estructuran de: un cuantificador, clase o término sujeto, verbo ser, clase o término predicado.
P2.2 Todo silogismo es argumento que tiene tres términos.
Los silogismos están estructurados con: la premisa mayor que recibe ese nombre ya que contiene al término mayor (P) que aparece como predicado de la conclusión, la premisa menor obtiene ese nombre por contener al término menor (S) que aparece como sujeto en la conclusión, el término medio que aparece en las dos premisas pero nunca en la conclusión.
P2.3 Todo silogismo es argumento que se puede validar con reglas y analogías.
Cualquier silogismo puede fallar en establecer su conclusión de distintas formas, por lo que se plantean seis reglas que pueden guiar al razonador. Se da muchas veces que tenemos un razonamiento en la forma típica de un silogismo, pero no es posible distinguir si las conclusiones son válidas o inválidas, para esto se debe emplear la ayuda de las analogías lógicas, que en base a silogismos preestablecidos son capaces de dilucidar cualquier inconveniente con respecto a un pensamiento referente a cualquier tema.
P3.1 Ningún silogismo es Sorites.
El sorites es una cadena de silogismos categóricos conectados por la conclusión del primero del primero, la cual es una premisa del segundo. Esta cadena sólo tiene dos eslabones, pero argumentos más extensos pueden constar de un número mayor.
P3.2 Ningún Silogismo es Dilema.
El dilema es una forma común de argumento en lenguaje cotidiano, una herramienta argumentativa en la que se combinan silogismos del mismo tema, en ocasiones con un efecto devastador.
P4.1 Algún silogismo según su tipo de premisas es Entimema
Los argumentos silogísticos ocurren con frecuencia, pero sus premisas y conclusiones no siempre se enuncian explícitamente. A menudo sólo una parte del argumento se expresa, el resto se “sobreentiende”.
P4.2 Algún silogismo según su tipo de premisas es silogismo disyuntivo.
Contienen una premisa compuesta disyuntiva (o alternativa), que afirma la verdad de al menos una de dos alternativas y una premisa que afirma la falsedad de una de las alternativas. Por ejemplo:
O bien P es verdad o bien Q es verdad.
P no es verdad.
Por lo tanto, Q es verdad.
P4.3 Algún silogismo según su tipo de premisas es silogismo hipotético.
Contienen una o más proposiciones compuestas hipotéticas (o condicionales), que afirman si uno de sus componentes (el antecedente) es verdad, entonces del otro componente (el consecuente) es verdad. Se distinguen dos subtipos.
P4.3.1 Algún silogismo según su tipo de premisas es silogismo hipotético puro.
Contienen únicamente proposiciones condicionales. Por ejemplo:
Si P es verdad, entonces Q es verdad.
Si Q es verdad, entonces R es verdad.
Por lo tanto, si P es verdad entonces R es verdad.
P4.3.2 Algún silogismo según su tipo de premisas es silogismo hipotético mixto.
Contiene una premisa condicional y una premisa categórica.
Si la premisa categórica afirma la verdad del antecedente de la premisa condicional y el consecuente de esa premisa condicional es la conclusión del argumento la forma es válida y se llama modus ponens. Por ejemplo:
Si P es verdad, entonces Q es verdad.
P es verdad.
por lo tanto, Q es verdad.
Si la premisa categórica afirma la falsedad del consecuente de la premisa condicional y la falsedad del antecedente de esa premisa condicional es la conclusión del argumento, la forma es válida y se llama modus tollens. He aquí un ejemplo:
Si P es verdad entonces Q es verdad.
Q es falsa.
Por lo tanto, P es falsa.
P.4.4.1 Algún silogismo según su traducción es silogismo categórico en forma estándar.
Silogismo categórico en el cual las premisas y la conclusión son proposiciones categóricas de forma estándar (A, E, I u O) y están ordenadas con la premisa mayor, luego premisa menor y al final la conclusión. Contienen únicamente proposiciones categóricas que afirma en un niegan la inclusión exclusión de categorías. Por ejemplo:
Todos los M son P
Todos los S son M
Por lo tanto, todos los S son P
P.4.4.2 Algún silogismo según su traducción es silogismo en lenguaje ordinario.
Los argumentos silogísticos en lenguaje ordinario pueden desviarse de los silogismos categóricos de forma estándar no sólo porque puede parecer que contienen más de tres términos, sino también porque las proposiciones componentes de los silogismos en lenguaje ordinario pueden no ser todas proposiciones de forma estándar.