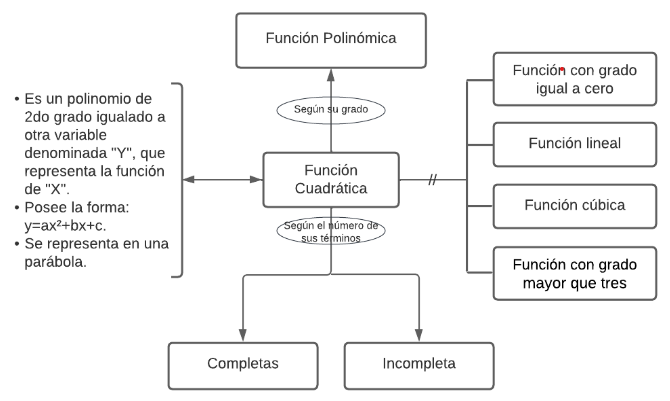
Mentefacto función cuadrática
Paquete proposicional
Supraordinadas
P1: Toda función cuadrática, según su grado, es función polinómica.
Isoordinadas
P2.1: Toda función cuadrática es un polinomio de 2do grado igualado a otra variable denominada “Y”, que representa la función de “X”.
P2.2: Toda función cuadrática es una función polinómica la cual posee la forma: y=ax²+bx+c.
P.2.3: Toda función cuadrática es una función que se representa en una parábola.
Exclusiones
P3.1: Ninguna función cuadrática es función con grado igual a cero.
P3.2: Ninguna función cuadrática es función lineal.
P3.3:Ninguna función cuadrática es función cúbica.
P3.4:Ninguna función cuadrática es función con grado mayor que tres.
Infraordinadas
P.4.1 Alguna función cuadrática, según el número de sus términos, es función cuadrática Completa.
P4.2 Alguna Función Cuadrática, según el número de sus términos, es función Cuadrática Incompleta.
Mentefactos proposicionales
- Mentefactos Proposicionales
P1: Toda función cuadrática, según su grado, es función polinómica.
P2.1: Toda función cuadrática es un polinomio de 2do grado igualado a otra variable denominada “Y”, que representa la función de “X”.
P2.2: Toda función cuadrática es una función polinómica la cual posee la forma: y=ax²+bx+c.
P.2.3: Toda función cuadrática es una función que se representa en una parábola.
P3.1: Ninguna función cuadrática es función con grado igual a cero.
P3.2: Ninguna función cuadrática es función lineal.
P3.3:Ninguna función cuadrática es función cúbica.
P3.4:Ninguna función cuadrática es función con grado mayor que tres.
P.4.1 Alguna función cuadrática, según el número de sus términos, es función cuadrática Completa.
P4.2 Alguna Función Cuadrática, según el número de sus términos, es función Cuadrática Incompleta.
Argumentaciones
P1. Toda función cuadrática, según su grado, es función polinómica.
Una función polinómica recibe su nombre debido a que está compuesta por un polinomio que puede ser de cualquier grado, y se define como aquella función cuya expresión algebraica se puede expresar como la suma o resta de un número finito de términos de diferente grado. En otras palabras, una función polinómica es una función que puede ser representada por un polinomio de la forma a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0, donde "a" son los coeficientes y "n" es el grado del polinomio.
La función cuadrática es un tipo particular de función polinómica que se forma a partir de un polinomio de segundo grado. Esta función se expresa como ax^2 + bx + c, donde "a", "b" y "c" son coeficientes constantes.
P2.1. Toda función cuadrática es un polinomio de 2do grado igualado a otra variable denominada “Y”, que representa la función de “X”.
La función cuadrática es la representación de valores dentro de una parábola por medio de la relación entre variables de X y Y, tomando en cuenta que para formar una función siempre se tendrá un polinomio igualado a la variable que queramos ubicar en el plano cartesiano.
P2.2. Toda función cuadrática es una función polinómica la cual posee la forma: y=ax²+bx+c.
Donde "y" representa la imagen o resultado de la función para un valor dado de "x", y "a", "b" y "c" son constantes. Esta ecuación puede ser representada gráficamente como una parábola. La variable "x" es la variable independiente y "y" es la variable dependiente en la función cuadrática. Donde ax² es el término cuadrático, bx es el término lineal lineal y c es el término independiente.
P.2.3. Toda función cuadrática es una función que se representa en una parábola.
La forma de la parábola depende del signo del coeficiente a en la función cuadrática. Si a es positivo, la parábola se abre hacia arriba (convexa), y si a es negativo, la parábola se abre hacia abajo (cóncava). Se denomina al vértice de la parábola como el punto más bajo o más alto si la parábola se abre hacia abajo.
P3.1. Ninguna función cuadrática es función con grado igual a cero.
Una función cuadrática es una función polinómica de segundo grado, lo que significa que el grado de la función es 2. Por lo tanto, la función cuadrática siempre tendrá una potencia de x elevada al menos al grado 2 en su expresión algebraica. Una función constante, por otro lado, es un polinomio de grado cero, lo que significa que su expresión algebraica no incluye ninguna potencia de x.
P3.2. Ninguna función cuadrática es función lineal.
Una función lineal tiene la forma f(x) = mx + b, donde m y b son constantes reales. La gráfica de una función lineal es una línea recta.
Por otro lado, una función cuadrática tiene la forma f(x) = ax^2 + bx + c, donde a, b, y c son constantes reales y a no es igual a cero. La gráfica de una función cuadrática es una parábola.
Como se puede ver, la forma de una función cuadrática es significativamente diferente a la forma de una función lineal, y las gráficas de estas dos funciones son diferentes. Por lo tanto, podemos concluir que ninguna función cuadrática es una función lineal.
P3.3. Ninguna función cuadrática es función cúbica.
Además de diferenciarse por su grado cada una con grado 2 y 3 respectivamente, Las funciones cuadráticas tienen una curvatura que describe una parábola, mientras que las funciones cúbicas tienen una curvatura más pronunciada que describe una curva suave, que puede tener dos puntos de inflexión. Además, las funciones cuadráticas tienen una sola raíz (punto donde la función cruza el eje x) mientras que las funciones cúbicas pueden tener hasta tres raíces.
P3.4. Ninguna función cuadrática es función con grado mayor que tres.
Las funciones de grado mayor que 3 tienden a tener formas más complejas y curvas más pronunciadas que las funciones cuadráticas, lo que las hace más adecuadas para modelar situaciones más complejas. Las funciones cuadráticas, por otro lado, son útiles para modelar situaciones en las que se necesita una curva suave, como en la trayectoria de un objeto lanzado en el aire o en la forma de un arco.
Referencias
- ¿Qué es una Función Polinómica? (ejemplos, tipos, gráfica, propiedades,...). (2021, March 16). Funciones Matemáticas. https://www.funciones.xyz/funcion-polinomica/
- Función cuadrática. (n.d.). Www.varsitytutors.com. https://www.varsitytutors.com/hotmath/hotmath_help/spanish/topics/quadratic-function
- Gráficas de las funciones polinómicas de grado menor o igual que 3. Cuadro resumen. (n.d.). Recursostic.educacion.es. Retrieved April 20, 2023, from http://recursostic.educacion.es/descartes/web/materiales_didacticos/Funciones_polinomicas_d3/resumen.htm#:~:text=En%20general%20las%20funciones%20polin%C3%B3micas
- LA FUNCIÓN CUADRÁTICA. (n.d.). https://www.uv.es/lonjedo/esoProblemas/3eso12funcioncuadratica.pdf
- LaEdu.digital. (2022, March 25). Funciones polinomiales de grado cero, uno y dos. Estudia En Línea. https://laedu.digital/2022/03/25/funciones-polinomiales-de-grado-cero-uno-y-dos/