Mentefacto Circunferencia
Paquete proposicional
Supraordinada
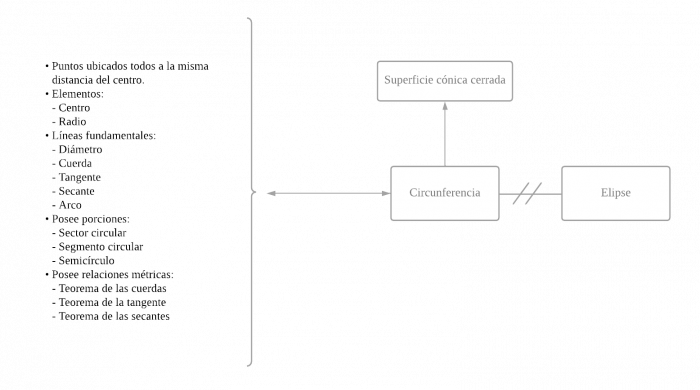
P.1: Toda circunferencia es una superficie cónica cerrada.
Isoordinadas
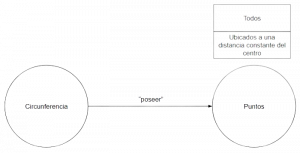
P.2.1: Toda circunferencia posee todos sus puntos ubicados a la misma distancia del centro.
P2.2: Toda circunferencia es poseedor de elementos.
P2.3: Toda circunferencia posee líneas fundamentales.
P.2.4: Toda circunferencia posee porciones.
P.2.5: Toda circunferencia posee relaciones métricas.
Exclusiones
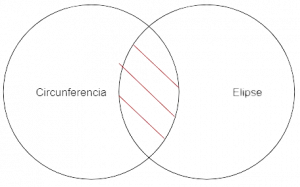
P.3: Ninguna circunferencia es elipse.
Mentefactos proposicionales
Argumentaciones.
P.1: Toda circunferencia es una superficie cónica cerrada.
Argumentación: Porque la circunferencia corresponde a la sección producida por un plano, que en este caso sería uno vertical al eje, una línea completamente vertical y fija, la cual es cortada por otra de modo oblicuo, conocido como generatriz, que gira alrededor de ella, generando así una superficie cónica (Imagen 1). Al producirse esta intersección, se produce también una línea curva cerrada, por lo que corresponde a una superficie de este tipo. (Imagen 2)
P.2.1: Toda circunferencia posee todos sus puntos ubicados a una distancia constante del centro.
Argumentación: Porque la circunferencia cuenta con un punto fijo llamado centro y una distancia fija llamada radio, las cuales nacen a partir de la intersección del plano secante perpendicular al eje, siendo el primero un punto de esta recta y la segunda la distancia del eje a la generatriz, provocando así que esta figura geométrica esté estructurada por un conjunto de todos los puntos en un plano que están a una distancia igual al radio del centro, que se encuentran ubicados consecuentemente, formando así una línea curva cerrada.
P2.2: Toda circunferencia posee elementos.
Argumentación: Porque la circunferencia, al ser un tipo de superficie cónica, cerrada cumple con sus características y elementos fundamentales, como:
- Radio: Segmento de una circunferencia que nace del centro y toca cualquier punto de la misma, el cual tiene un valor constante. A su vez, este puede ser considerado como una línea fundamental, pero bajo el criterio de superficie cónica, se lo considera como un elemento fundamental también.
- Centro: Punto dentro de la circunferencia que está a la misma distancia que todos los puntos que conforman a la línea cerrada.
P2.3: Toda circunferencia posee líneas fundamentales.
Argumentación: Porque la circunferencia, al ser un tipo de superficie cónica cerrada cumple, con todas sus líneas fundamentales, las cuales son:
- Diámetro: Une dos puntos de una circunferencia, pasando por el centro. Hay infinitos diámetros y todos pasan dicho punto de la circunferencia. Se la puede considerar como una cuerda. Puede formar junto a un radio o a otro diámetro, dos o un ángulo central respectivamente.
- Cuerda: Segmento de recta que une dos puntos cualquiera de una circunferencia. Dos cuerdas forman un ángulo inscrito si tienen un punto en común, caso contrario, forman dos ángulos interiores.
- Tangente: Recta que toca a la circunferencia en un solo punto y es perpendicular a un radio.
- Secante: Recta que corta dos puntos cualesquiera de la línea de una circunferencia. La diferencia con la cuerda, es que una secante tiene sus extremos prolongados. Puede formar un ángulo semi inscrito con una cuerda. Si dos extremos de dos secantes diferentes se intersecan, formando un ángulo exterior.
- Arco: Todas las las partes en que una cuerda divide a la circunferencia. Por cada de estas líneas, existirían dos arcos.
- Flecha: Es el segmento que une el punto medio de un arco al punto medio de la cuerda que lo forma.
P.2.4: Toda circunferencia posee porciones.
Argumentación: Porque la circunferencia, al ser un tipo de superficie cónica cerrada cumple, con porciones, las cuales son:
- Sector circular: Es el área de círculo que se forma entre dos radios y el arco de circunferencia frente a ellas.
- Segmento circular: Es la región formada entre una cuerda y el arco de circunferencia frente a ella.
- Semicírculo: Es el área delimitada por un diámetro en la circunferencia y cualquiera de las dos semicircunferencias que se establecen alrededor de ella.
P.2.5: Toda circunferencia posee relaciones métricas.
Argumentación: Porque la circunferencia al ser un tipo de superficie cónica cerrada, cumple con relaciones métricas que se basan en la relación entre la longitud de la circunferencia y su diámetro.
- Teorema de las cuerdas: Afirma que si dos cuerdas se intersectan dentro de una circunferencia, entonces el producto de las longitudes de los segmentos de cada una de las cuerdas es igual.
- Teorema de la tangente y la secante: Afirma que si una tangente y una secante a una circunferencia se intersectan en un punto exterior a ella, entonces el producto de las medidas de los segmentos determinados por el punto exterior y los dos puntos de intersección de la secante con la circunferencia es igual al cuadrado de la medida del segmento de tangente determinado por el punto exterior y el punto de tangencia.
- Teorema de las secantes: Afirma que si dos secantes a una circunferencia se intersectan fuera de ella, entonces los productos de las medidas de los segmentos que, en cada secante, determinan el punto exterior y los dos puntos de intersección con la circunferencia son iguales.
P.3: Ninguna circunferencia es elipse.
Argumentación: Las elipses, al contrario de las circunferencias, intersecan un plano no perpendicular al eje, causando que sus puntos no estén a la misma distancia del centro, por lo que son curvas cerradas y definidas definidas por dos ejes, tienen dos focos, puntos equidistantes del centro, dando a entender que tiene algunos elementos inéditos. Además, sus líneas notables cambian de definición, y sus relaciones métricas son diferentes a la de la circunferencia, así como sus porciones.
Referencias
Alonso, M. (2020). Introducción_Cónicas. Recursostic.educacion.es. http://recursostic.educacion.es/descartes/web/materiales_didacticos/Las_conicas_como_lugares_geometricos/Las_conicas_como_lugares_geometricos.htm#:~:text=La%20superficie%20c%C3%B3nica%20de%20revoluci%C3%B3n
CECyT 3. (2015). Concepto de circunferencia y sus elementos. Www.cecyt3.Ipn.mx. https://www.cecyt3.ipn.mx/ibiblioteca/mundodelasmatematicas/ConceptoDeCircunferenciaYSusElementos.html
COLEGIO INTEGRADO SAN PIO X – TALCA. (2020). COLEGIO INTEGRADO SAN PIO X -TALCA DEPARTAMENTO DE MATEMÁTICA. https://www.colegiointegrado.cl/trabajando_casa/GUIAS/IV/1%20SEMANA%2018-20/ELECTIVO%20MATEM%C3%81TICA.pdf
Guzman, J. (2021, April 26). Elementos y Partes de la Elipse con Diagramas. Neurochispas. https://www.neurochispas.com/wiki/elementos-de-la-elipse/
Marta. (2021). Todo sobre las conicas | Superprof. Material Didáctico - Superprof. https://www.superprof.es/apuntes/escolar/matematicas/analitica/conica/conicas.html
Sangaku Maths. (2018). Definición y elementos básicos de la circunferencia. Www.sangakoo.com. https://www.sangakoo.com/es/temas/definicion-y-elementos-basicos-de-la-circunferencia
Unibetas. (2022, March 15). Elementos de la circunferencia: ejemplos y ejercicios resueltos. Unibetas Curso Examen de Admisión Online. https://unibetas.com/elementos-circunferencia