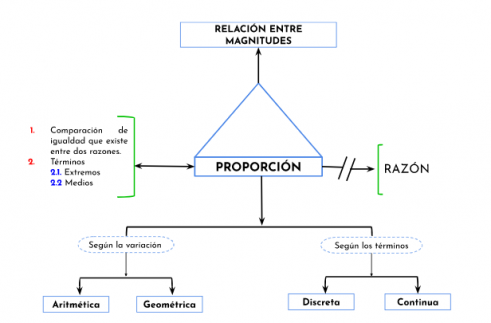
Mentefacto proporcion
Paquete proposicional:
Pp1 La proporción es relación entre magnitudes.
Pp.2.1 La proporción es una igualdad entre dos razones.
Pp.2.2 La proporción tiene términos extremos.
Pp.2.3 La proporción tiene términos medios.
Pp.3 La Proporción es razón.
Pp.4.1 Las Proporciones son proporciones aritméticas.
Pp.4.2 Las proporciones son proporciones geométricas.
Pp.4.3 La Proporción es una proporción directa.
Pp.4.4 La proporción es proporción continua.
Análisis proposicional
Pp1 La proporción es relación entre magnitudes.
Argumentación: La proporción es una conexión entre cuatro cantidades que provienen de magnitudes.
Ejemplo:
- Maria es dos años mayor que Ana como José es mayor que Luis.
- Luis tiene el doble de dinero que pepito como Anibal tiene el doble que Alicia.
- Para preparar arroz, por cada taza de arroz hay dos de agua como por cada 3 tazas de arroz hay que poner 6 de agua.
- 10 de cada niños tienen tablet como 9 de cada 30 tienen juguetes electrónicos.
Pp.2.1 La proporción es una igualdad entre dos razones.
Argumentación: Cuando dos razones tienen el mismo valor, se dice que guarda la misma proporción o que dichas razones son equivalentes, por lo tanto, al igualarlas se forman lo que se denomina una proporción.
Ejemplo:
7/3 = 14/6 = 2 , 3
Proporción
Constante de proporcionalidad
10/50 = 5/25 = 0 , 2
Proporción
Pp.2.2 La proporción tiene términos extremos.
Argumentación: Porque los componentes de una proporción se llaman extremos y medios. Los extremos: son el primer y el último término de la proporción.
Pp.2.3 La proporción tiene términos medios.
Argumentación: Porque los componentes de una proporción se llaman extremos y medios. Los medios:están entre los extremos,es decir segundo y tercer término.
Pp.3 La Proporción no es Razón.
Argumentación: Las relaciones que se establece en las razones son comparaciones entre dos cantidades y en las proporciones es de 4 cantidades.
Pp.4.1 Las Proporciones son proporciones aritméticas. Argumentación: una proporción aritmética es una igualdad entre dos razones aritméticas se llaman EQUIDIFERENCIAS.
Ejemplo:
Símbolos matemáticos lenguaje cotidiano
| 12 - 5 = 9 - 2 | Tania tiene 3 dólares más que Eliana como Said tiene 3 dólares más que Andrés. |
| 42 - 36 = 65 - 49 | Leo es mayor que Alex por 6 como Liliana es 6 años mayor que elena |
Pp.4.2 Las proporciones son proporciones geométricas.
Argumentación: Una proporción geométrica es una igualdad entre dos razones geométricas
Ejemplo:
3/4 = 9/12 3. 12 = 4.9 3 . 12 = 4.9 3/4 = 9/12 30/15 = 6/3 30 . 3 =15.6 30 . 3 =15.6 30/15 = 6/3
Pp.4.3 Alguna Proporción es una proporción directa.
Argumentación: Proporción discreta es aquella en la cual sus cuatro términos son diferentes entre sí.
Ejemplo:
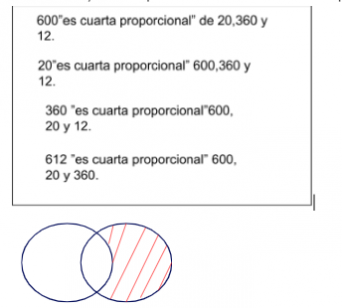
600 km/ 20 km = 360 km / 12 km
Es una Proporción geométrica discreta se denomina “ cuarta proporcional” a cada uno de sus términos y se dice que cada uno de ellos es “cuarta proporcional” de los otros tres.
Pp.4.4 La proporción es proporción continua.
Argumentación: Proporción continua es aquella en la cual sus términos medios o términos extremos son iguales.
Ejemplo:
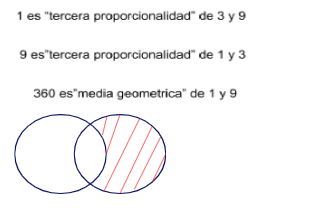
1 km/3 min = 3km/9 min
Es una proporción geométrica continua se denomina “ tercera proporcional” a cada uno de sus términos no iguales y “ media proporcionalidad” o media geométrica al término que se repite. Así: