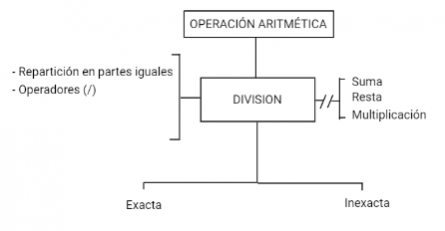
Mentefacto División
Paquete Proposicional
Supraordinada
P1. Toda división es operación aritmética.
Isoordinadas
P2.2. Toda división es operación con operadores.
Infraordinadas
P3.1 Alguna división es exacta.
P3.2 Alguna división es inexacta.
Exclusiones
P4.1. Ninguna división es suma.
P4.2. Ninguna división es resta.
P4.3. Ninguna división es multiplicación.
Argumentaciones
P1. Toda división es operación aritmética.
La división se considera una operación aritmética porque cae dentro de la rama de las matemáticas conocida como aritmética, que se ocupa de las operaciones numéricas básicas como la suma, la resta, la multiplicación y la división. La aritmética se enfoca en la manipulación de números para realizar cálculos y resolver problemas relacionados con cantidades, medidas y cálculos que involucran números reales.
P2.1. Toda división es operación de reparticiones iguales.
La división a menudo se denomina "parte igual" porque implica dividir una cantidad o un todo en partes que son equivalentes o de igual tamaño. Cuando se divide un número o un objeto en partes iguales, cada parte representa una parte igual de la cantidad original o total.
P2.2. Toda división es operación con operadores.
La división, al igual que otras operaciones matemáticas, se representa mediante operadores para proporcionar una forma estandarizada y concisa de realizar la operación y expresar relaciones matemáticas. Los operadores son símbolos o notaciones que representan operaciones matemáticas y se utilizan en la notación matemática para denotar operaciones específicas.
P3.1 Alguna división es exacta.
La división es exacta cuando la operación de división da como resultado un cociente exacto sin resto. Esto significa que el resultado de la división es un número entero y no sobra ningún resto.
P3.2 Alguna división es inexacta.
La división es generalmente precisa cuando se realiza de acuerdo con las reglas y propiedades de la aritmética. Sin embargo, hay ciertos escenarios o situaciones donde la división puede ser inexacta o indefinida, por ejemplo cuando es un número irracional.
P4.1. Ninguna división es suma.
La división es una operación matemática que consiste en dividir una cantidad en partes iguales o grupos. Es el proceso de averiguar cuántas veces se puede restar una cantidad (el divisor) de otra cantidad (el dividendo) para obtener un cociente, que puede ser un número entero, una fracción o un decimal, por otro lado, la suma es una operación matemática que consiste en combinar dos o más cantidades para obtener un resultado.
P4.2. Ninguna división es resta.
La división es una operación matemática que consiste en dividir una cantidad en partes iguales o grupos. Es el proceso de averiguar cuántas veces se puede restar una cantidad (el divisor) de otra cantidad (el dividendo) para obtener un cociente, que puede ser un número entero, una fracción o un decimal, por otro lado, la resta es una operación matemática que consiste en encontrar la diferencia entre dos cantidades. Representa el concepto de "quitar" o "quitar" una cantidad de otra cantidad para obtener un resultado.
P4.3. Ninguna división es multiplicación.
La multiplicación es una operación matemática que consiste en combinar dos o más cantidades (llamadas factores) para obtener un producto y representa el concepto de adición repetida o agrupación de cantidades, por otro lado, la división es una operación matemática que consiste en dividir una cantidad en partes iguales o grupos y es el proceso de averiguar cuántas veces se puede multiplicar una cantidad (el divisor) por otra cantidad (el cociente) para obtener el dividendo.