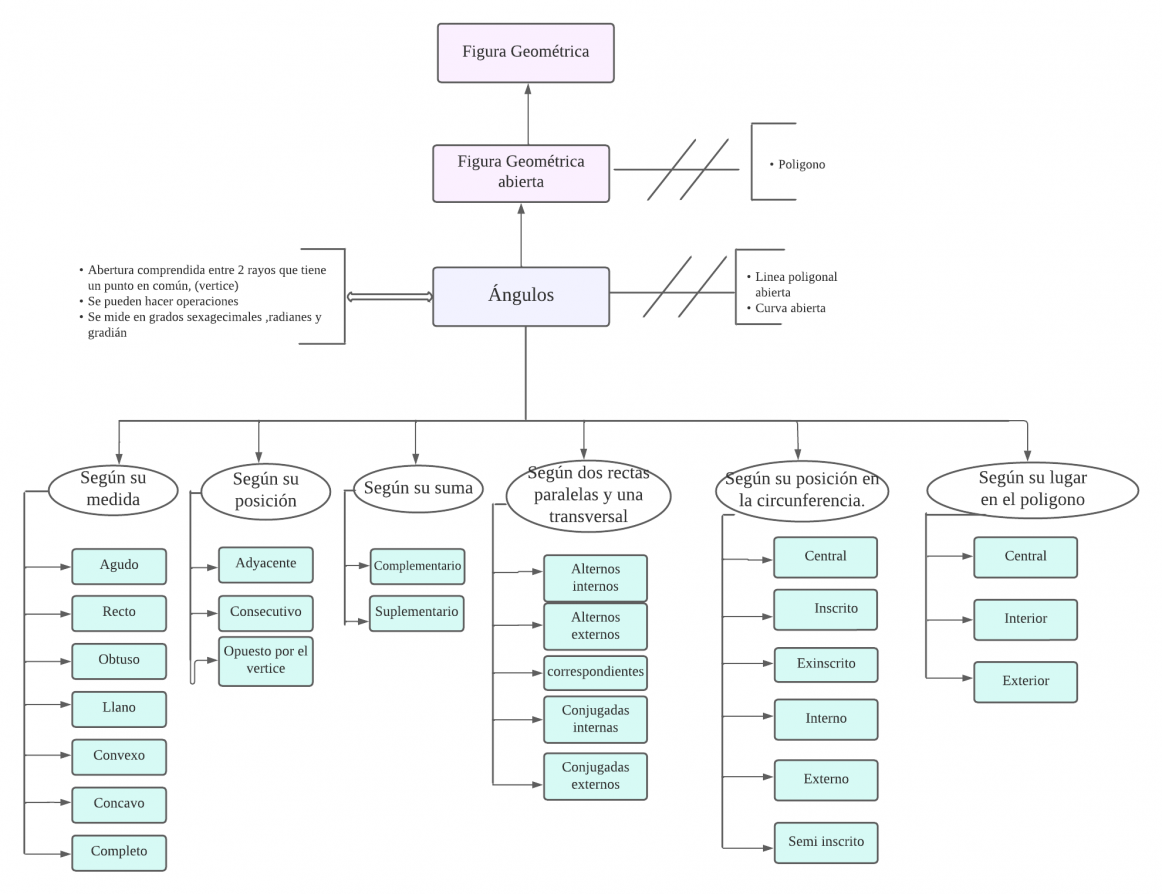
Mentefacto de los Ángulos
Paquete proposicional
Supraordinada
P.1- Todo ángulo es figura geométrica abierta.
P1.1.-Todo ángulo es figura geométrica.
Isoordinada
P2.- El ángulo es una abertura comprendida entre 2 rayos unidos por un vértice.
P2.1.- Todo ángulo es figura geométrica abierta operable.
P.2.2.- Todo ángulo es figura medida en grados sexagecimales, radianes y gradianes.
Exclusión
P.3- Ningún ángulo es línea poligonal abierta.
P.3.1.- Ningún ángulo es curva abierta.
P3.2.- Ningúna figura geométrica abierta es poligono.
Infraordinada
P4.- Según su medida, algunos ángulos son ángulos agudos.
P4.1.- Según su medida, algunos ángulos son ángulos rectos.
P.4.2.- Según su medida, algunos ángulos son ángulos obtusos.
P.4.3.- Según su medida, algunos ángulos son ángulos llanos.
P.4.4.-Según su medida, algunos ángulos son ángulos convexos.
P.4.5.- Según su medida, algunos ángulos son ángulos cóncavos.
P.4.6.-Según su medida, algunos ángulos son ángulos completos.
P.5.- Según su posición, algunos ángulos son ángulos adyacentes.
P. 5.1.- Según su posición, algunos ángulos son ángulos consecutivos
P.5.2.- Según su posición, algunos ángulos son ángulos opuestos por el vértice.
P.6.- Según su suma, algunos ángulos son ángulos complementarios.
P.6.1.- Según su suma, algunos ángulos son ángulos suplementarios.
P.7.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos alternos internos.
P.7.1.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos alternos externos.
P.7.2.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos correspondientes.
P.7.3.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos conjugada internas.
P.7.4.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos conjugados externos.
P.8.- Según su posición en la circunferencia, algunos ángulos son ángulos central.
P.8.1- Según su posición en la circunferencia, algunos ángulos son ángulos inscrito.
P.8.2- Según su posición en la circunferencia, algunos ángulos son ángulos exinscrito.
P.8.3.- Según su posición en la circunferencia, algunos ángulos son ángulos interno.
P.8.4.- Según su posición en la circunferencia, algunos ángulos son externos.
P.8.5.- Según su posición en la circunferencia, algunos ángulos son ángulos semi- inscrito.
P.9.- Según su lugar en un polígono, algunos ángulos son ángulos centrales.
P.9.1.- Según su lugar en un polígono, algunos ángulos son ángulos interiores.
P.9.2- Según su lugar en un polígono, algunos ángulos son ángulos exterior.
- Mentefactos Proposicionales
Argumentaciones
P.1- Todo ángulo es figura geométrica abierta.
Un ángulo es una figura abierta porque no encierra una región en el plano, a diferencia de las figuras cerradas como los polígonos. El ángulo no tiene un área definida y no se puede calcular mediante fórmulas como en el caso de los triángulos o los cuadriláteros. Además de que no tiene una longitud o área definidas, su forma puede variar dependiendo de la medida de sus lados y no encierra una región en el plano. Un ejemplo de figura geométrica abierta es una línea recta o una curva, ya que estas formas geométricas no tienen un punto final y se extienden indefinidamente en una dirección determinada
P1.1.-Todo ángulo es figura geométrica.
Se ocupa para describir la relación entre dos líneas que se intersectan en un punto común. Un ángulo se mide en grados, y se define como la cantidad de rotación necesaria para llevar una línea hasta coincidir con la otra. El punto común donde se intersectan las dos líneas se llama vértice del ángulo. Sin embargo, se pueden utilizar distintas figuras geométricas para representar visualmente los ángulos. Por ejemplo, un ángulo puede ser representado como un sector circular, donde el vértice del ángulo es el centro del círculo y las dos líneas que forman el ángulo son los radios del sector. También se pueden utilizar triángulos, polígonos regulares y otros objetos geométricos para visualizar los ángulos.
P2.- El ángulo es una abertura comprendida entre 2 rayos unidos por un vértice.
Se define como ángulo la abertura comprendida entre dos rayos que tiene un punto en común, llamado vértice, es una forma precisa y útil de medir la separación o diferencia de dirección entre dos cuerpos o puntos en un plano. Además, esta definición permite distinguir entre diferentes tipos de ángulos, lo cual es importante en el estudio de la geometría. Por ejemplo, un ángulo recto tiene una abertura de 90°, mientras que un ángulo agudo tiene una abertura menor a los 90° y un ángulo obtuso tiene una abertura mayor a 90°.
P2.1.- Todo ángulo es figura geométrica abierta operable.
Un ángulo es una figura geométrica con la que se puede realizar operaciones matemáticas como sumas, restas, multiplicaciones y divisiones. Tomando en cuenta estas operaciones se puede realizar: La suma de dos o más ángulos se define como la medida del ángulo formado cuando dos ángulos son adyacentes de manera que el vértice de un ángulo coincide con el vértice del otro ángulo. La resta de ángulo se define como la medida del ángulo formado cuando la medida del primer ángulo se resta de la del segundo ángulo. La multiplicación y división de ángulos se utilizan en trigonometría, específicamente dentro de las funciones trigonométricas. Por ejemplo, la función trigonométrica Seno de un ángulo α es una función trigonométrica cuya fórmula se define como la razón entre el cateto opuesto y la hipotenusa de un triángulo rectángulo (triángulo con un ángulo recto).
P.2.2.- Todo ángulo es figura medida en grados sexagecimales, radianes y gradianes.
Para medir esta abertura o separación angular, se utilizan diferentes unidades de medida, que nos permiten expresar el ángulo en diferentes sistemas de medición como lo es: El sistema de medición de ángulos más utilizado es el sistema sexagesimal: basado en la división de un ángulo completo en 360 partes iguales, cada una de ellas denominada grado sexagesimal. Así, un ángulo de 90 grados sexagesimales se representa como 90°.Otra unidad de medida que se utiliza para medir ángulos es el radián, que se define como la medida del ángulo central que tiene un arco de circunferencia de la misma longitud que el radio de la circunferencia. Un ángulo de 1 radián se define como aquel que abarca un arco de longitud igual al radio de la circunferencia. De esta forma, un ángulo de 90 grados sexagesimal se corresponde con un ángulo de π/2 radianes. La tercera unidad de medida que se utiliza para medir ángulos es el grado centesimal o gradian. Este sistema se basa en la división de un ángulo completo en 400 partes iguales, cada una de ellas denominada grado centesimal o gradian. Así, un ángulo de 90 grados sexagesimales se representa como 100 gradianes. entre el lado opuesto de un ángulo agudo de un triángulo rectángulo y la hipotenusa.
P.3- Ningún ángulo es línea poligonal abierta
En la geometría, una línea poligonal abierta se define como una figura geométrica formada por segmentos de recta consecutivos que se unen en sus extremos para formar una figura abierta. Mientras que el ángulo es una figura geométrica abierta que se forma cuando dos rayos se extienden desde un mismo punto, llamado vértice, hacia diferentes direcciones. Una línea poligonal abierta está formada por segmentos de recta consecutivos, el ángulo está formado por dos rayos que se extienden desde un mismo punto, eso quiere decir que no tiene segmentos de recta como componentes. Además, otra diferencia importante es que los ángulos tienen una medida asociada, mientras que las líneas poligonales abiertas no. La medida del ángulo se expresa en grados sexagesimales, radianes o gradianes y representa la abertura entre los dos rayos que forman el ángulo. Por ejemplo, un ángulo tiene una medida en grados, mientras que una línea poligonal abierta no tiene medida definida, ya que puede ser infinitamente larga o corta.
P.3.1.- Ningún ángulo es curva abierta.
En geometría, una curva abierta se define como una figura geométrica formada por una línea continua que no se cierra sobre sí misma, es decir que posee extremos abiertos. Ahora, el ángulo es una figura geométrica abierta que se forma cuando dos rayos se extienden desde un mismo punto, llamado vértice, hacia diferentes direcciones. Una curva abierta es una línea continua que no se cierra sobre sí misma, el ángulo está formado por dos rayos que se extienden desde un mismo punto, lo que significa que no es una línea continua, otra diferencia importante es que las curvas abiertas pueden tener una longitud medida, mientras que los ángulos tienen una medida asociada que representa la abertura entre los dos rayos que forman el ángulo. Como por ejemplo podrá formar parábolas, hipérbolas y curvas sinusoidales.
P3.2.- Ningúna figura geométrica abierta es poligono.
Una figura geométrica abierta no es considerada un polígono en geometría debido a que no es una figura cerrada formada por una secuencia finita de segmentos de recta llamados lados, que se unen en sus extremos para formar una figura cerrada. Las figuras geométricas abiertas son importantes en geometría y en muchas otras áreas de las matemáticas y la física debido a sus propiedades únicas. Un ejemplo de figura geométrica abierta es una línea curva, como una circunferencia, que tiene una sola arista y no es un polígono porque no es una figura cerrada. Otro ejemplo de figura abierta es un conjunto de segmentos de recta no conectados entre sí, como una estrella de cinco puntas.
P4.- Según su medida, algunos ángulos son ángulos agudos.
Un ángulo se considera agudo cuando su medida es menor a 90°. Esto significa que los dos rayos que forman el ángulo están relativamente cerca uno del otro y no se extienden en direcciones opuestas. Ejemplos de ángulos agudos incluyen el ángulo formado por las manecillas de un reloj a las 3:00 y el ángulo formado por la línea del horizonte y la línea de un árbol en un paisaje.
P4.1.- Según su medida, algunos ángulos son ángulos rectos.
Un ángulo se considera recto cuando su medida es exactamente 90° esto significa que los dos rayos que forman el ángulo son perpendiculares entre sí y forman una esquina en el vértice del ángulo. Es importante destacar que los ángulos rectos tienen muchas propiedades y aplicaciones importantes en la geometría y otras áreas de las matemáticas y la física. Por ejemplo, en trigonometría, los ángulos rectos se utilizan para definir las funciones trigonométricas básicas, como el seno, el coseno y la tangente.
P.4.2.- Según su medida, algunos ángulos son ángulos obtusos.
En particular, un ángulo se considera obtuso cuando su medida es mayor que 90 grados, pero menor que 180 grados. Esto significa que los dos rayos que forman el ángulo se extienden más allá de una línea recta y se abren en una dirección opuesta a la de un ángulo agudo. Estos tienen algunas propiedades y aplicaciones importantes en la geometría y otras áreas de las matemáticas y la física. Por ejemplo, en trigonometría, los ángulos obtusos se utilizan para definir funciones trigonométricas y resolver ecuaciones trigonométricas complejas, también son importantes en la construcción de figuras geométricas, como triángulos y polígonos. En estas figuras, los ángulos obtusos permiten que las líneas se corten en ángulos mayores que 90 grados y formen figuras con lados y ángulos congruentes.
P.4.3.- Según su medida, algunos ángulos son ángulos llanos.
Un ángulo se considera llano cuando su medida es de exactamente 180 grados. Es decir que los dos rayos que forman el ángulo se extienden hasta formar una línea recta, destacando que los ángulos llanos tienen algunas propiedades y aplicaciones importantes en la geometría y otras áreas de las matemáticas y la física. Por ejemplo, en la construcción de figuras geométricas, los ángulos llanos son utilizados para crear polígonos con lados rectos y ángulos congruentes. También son importantes en la resolución de problemas y ecuaciones en la trigonometría y otras áreas de las matemáticas. O en la trigonometría, el concepto de ángulos llanos se utiliza para entender la relación entre senos, cosenos y tangentes, lo que es fundamental para la resolución de problemas en la vida diaria.
P.4.4.-Según su medida, algunos ángulos son ángulos convexos.
Un ángulo se considera convexo cuando su medida es menor a 180 grados. Esto significa que los dos rayos que forman el ángulo no se intersectan y están en la misma dirección. Es decir, en un ángulo convexo, los dos rayos que lo forman se extienden hacia afuera desde el vértice y no se curvan hacia adentro. Por lo tanto, la región interior del ángulo queda completamente contenida en un solo lado del ángulo. Los ángulos convexos son muy comunes en la geometría y en la vida cotidiana, y tienen varias propiedades importantes. Por ejemplo, los ángulos convexos son fundamentales en la construcción de polígonos, ya que todos los polígonos regulares tienen ángulos convexos congruentes. Además, en la trigonometría, la mayoría de los ángulos involucrados en problemas son ángulos convexos, ya que están en el rango de 0 a 180 grados.
P.4.5.- Según su medida, algunos ángulos son ángulos cóncavos.
Un ángulo es cóncavo cuando su amplitud es mayor a 180°, lo que significa que la abertura entre las dos rayos que lo conforman es "hacia adentro". Esta forma de clasificar los ángulos se utiliza en la geometría euclidiana, que es la rama de las matemáticas que estudia las propiedades de los objetos y figuras geométricas en un plano. Se puede entender como un ángulo que se "dobla" hacia el interior, en lugar de hacia afuera. Esta característica puede ser útil para describir la forma de algunos objetos, como los polígonos cóncavos, que tienen al menos un ángulo cóncavo. Como por ejemplo el ángulo obtuso es un ángulo mayor a 90 grados y menor a 180 grados. Este ángulo tiene una abertura hacia adentro y se forma cuando las dos líneas que lo componen se extienden hacia direcciones opuestas.
P.4.6.-Según su medida, algunos ángulos son ángulos completos.
La medida de un ángulo se puede expresar en grados, y un ángulo completo se define como aquel que mide 360°. Por lo que un ángulo completo es aquel que "da la vuelta completa" y vuelve a su posición inicial después de recorrer una circunferencia completa. Esta característica puede ser útil en diferentes situaciones, como en el estudio de la trigonometría y en la resolución de problemas geométricos más avanzados. Ejemplo: El reloj cumple ya que las manecillas de un reloj completan una vuelta completa cada 12 horas, es decir, cada 720 minutos. La medida del ángulo completo es de 360°.
P.5.- Según su posición, algunos ángulos son ángulos adyacentes.
En geometría, dos ángulos se consideran adyacentes cuando comparten un lado común y un vértice común, pero no comparten ningún interior. Esto significa que los dos ángulos están "juntos" en el plano, y su posición relativa es importante para determinar si son o no adyacentes. Por ejemplo, si tenemos dos ángulos que comparten un vértice común y un lado común, pero no tienen intersección en su interior, entonces se consideran adyacentes. Por otro lado, si dos ángulos se cruzan en su interior, entonces no son adyacentes. Es importante tomar en cuenta que dos ángulos adyacentes pueden tener medidas diferentes, y su posición relativa en el plano es lo que determina si son o no adyacentes.
P.5.1.- Según su posición, algunos ángulos son ángulos consecutivos.
Si dos ángulos se consideran consecutivos si tienen un vértice común y comparten un lado, pero no tienen ningún otro punto en común. Es decir los dos ángulos están uno al lado del otro en el plano, y su posición relativa es importante para determinar si son o no consecutivos. Por ejemplo, si tenemos dos ángulos que comparten un vértice común y un lado común, entonces se consideran consecutivos. Además, si tenemos tres ángulos consecutivos, entonces la suma de sus medidas es igual a 180 grados, ya que forman una línea recta. Es importante tener en cuenta que los ángulos consecutivos pueden tener medidas diferentes, y su posición relativa en el plano es lo que determina si son o no consecutivos.
P.5.2.- Según su posición, algunos ángulos son ángulos opuestos por el vértice.
Si tomamos dos de estos ángulos que comparten un vértice común, notaremos que los otros dos ángulos son opuestos por el vértice. Esto se debe a que, por definición, los ángulos opuestos por el vértice tienen los lados que son prolongaciones de los lados del ángulo inicial, pero que se encuentran en la dirección opuestas. Los ángulos opuestos por el vértice tienen la misma medida, lo que significa que son congruentes. Esto se debe a que, como mencioné anteriormente, sus lados son prolongaciones de los lados del ángulo inicial y, por lo tanto, tienen la misma longitud. Un ejemplo común de ángulos opuestos por el vértice se encuentra en las formas geométricas regulares, como el cuadrado. En un cuadrado, los cuatro ángulos interiores son iguales y miden 90 grados, y cada uno de estos ángulos opuestos por el vértice tiene la misma medida de 90 grados.
P.6.- Según su suma, algunos ángulos son ángulos complementarios.
Los ángulos son complementarios porque en la geometría plana, cuando dos ángulos se suman y el resultado es igual a 90 grados, se dice que son complementarios. Esto se debe a que 90 grados es la medida del ángulo recto, que es un ángulo muy importante en la geometría. Por lo tanto, si tenemos dos ángulos A y B, y A + B = 90 grados, entonces se dice que A y B son complementarios. Esta propiedad es muy útil en la resolución de problemas geométricos, ya que nos permite relacionar los ángulos de una figura y obtener información sobre ellos. Por ejemplo, si en un triángulo conocemos que uno de los ángulos es complementario a otro ángulo, podemos usar esta información para encontrar el valor del tercer ángulo.
P.6.1.- Según su suma, algunos ángulos son ángulos suplementarios.
Los ángulos son suplementarios porque en la geometría plana, cuando dos rectas se intersectan, los ángulos que se forman en el mismo lado de una de las rectas tienen una suma de 180 grados. Esta propiedad se conoce como el axioma del ángulo suplementario. En otras palabras, si tenemos dos ángulos A y B que están en el mismo lado de una recta y cuyos vértices están en esa recta, entonces A y B son suplementarios si A + B = 180 grados. Como por ejemplo de ángulos suplementarios serían dos ángulos que forman un ángulo llano.
P.7.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos alternos internos.
Estos ángulos se llaman "alternos internos", dos triángulos congruentes que se forman por la intersección de las rectas y la transversal. En estos triángulos, los lados paralelos son congruentes y los lados transversales son iguales. Por lo tanto, los ángulos opuestos a los lados paralelos también son congruentes, ya que los triángulos son congruentes. Debido a esto, se puede demostrar que los ángulos alternos internos son congruentes. Esta propiedad es útil en la resolución de problemas geométricos, ya que nos permite encontrar la medida de un ángulo desconocido en una figura cuando se conocen otros ángulos. Por ejemplo, una figura con dos rectas paralelas y una transversal, y se nos pide encontrar la medida de un ángulo desconocido, podemos utilizar la propiedad de los ángulos alternos internos para determinar la medida de este ángulo en función de otros ángulos conocidos.
P.7.1.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos alternos externos.
Llos alternos externos son aquellos que están ubicados en lados opuestos de la transversal, fuera de las dos rectas paralelas. Es decir, si consideramos dos ángulos en diferentes lados de la transversal, uno a la derecha de una de las rectas paralelas y el otro a la derecha de la otra recta paralela, entonces estos dos ángulos son alternos externos. La propiedad de los ángulos alternos externos se puede demostrar a través de la congruencia de triángulos. Si tomamos dos triángulos, uno formado por dos ángulos alternos externos y la transversal, y otro formado por dos ángulos internos y la transversal, podemos demostrar que ambos triángulos son congruentes. Esto se debe a que ambos triángulos tienen un ángulo en común (el ángulo de la transversal) y dos ángulos más que son iguales, ya que son ángulos correspondientes (uno interno y uno externo). Por lo tanto, los dos triángulos son iguales en todos sus lados y ángulos, lo que demuestra que los ángulos alternos externos son congruentes. Ejemplo: Los ángulos de la calle cuando dos calles se cortan en un cruce, los ángulos alternos externos se forman en las esquinas del cruce. Si las calles son paralelas, los ángulos alternos externos serán iguales.
P.7.2.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos correspondientes.
Entre estos ángulos se encuentran los llamados ángulos correspondientes, que son aquellos que se encuentran en el mismo lado de la transversal y en la misma posición relativa respecto a las rectas paralelas. En donde dos ángulos se consideran correspondientes si se encuentran en lados opuestos de la transversal y se encuentran en la misma posición respecto a las rectas paralelas. Es decir, si uno de los ángulos está por encima de la transversal y el otro por debajo, entonces son correspondientes si ambos se encuentran a la misma distancia respecto a las rectas paralelas. Estos ángulos reciben su nombre debido a que tienen la misma medida, por lo que son congruentes. Ejemplos: Los ángulos en forma de F como en un marco de puerta, los ángulos correspondientes se forman en los bordes del marco de la puerta y el borde de la pared.
P.7.3.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos conjugada internas.
Cuando una transversal cruza dos rectas paralelas, se forman ángulos en los puntos de intersección. Si se considera un punto en una de las rectas y se trazan dos segmentos desde ese punto a las dos rectas paralelas, se forman cuatro ángulos. Los ángulos que se encuentran del mismo lado de la transversal y en la misma posición son llamados ángulos conjugados internos. Estos ángulos tienen la misma medida y su suma es igual a 180 grados. Ejemplo: Ángulos de un paralelogramo los ángulos conjugados internos se encuentran en los lados opuestos del paralelogramo y son iguales.
P.7.4.- Según dos rectas paralelas y una transversal, algunos ángulos son ángulos conjugados externos.
Cuando dos rectas paralelas son intersecadas por una tercera recta transversal, los ángulos que se encuentran en el exterior de las rectas paralelas y en el mismo lado de la transversal se llaman ángulos conjugados externos. Estos ángulos son iguales entre sí, es decir, si uno de los ángulos conjugados externos mide x grados, entonces el otro ángulo conjugado externo también medirá x grados. La suma de estos dos ángulos conjugados externos siempre será 180 grados. Esto puede ser demostrado mediante el uso de la propiedad de que la suma de los ángulos interiores de un triángulo es 180 grados. Al dibujar dos triángulos en el interior de las rectas paralelas y la transversal, se pueden observar los ángulos que son iguales y cuya suma es igual a 180 grados. Ejemplo: Ángulos en un trapecio los ángulos conjugados externos se encuentran en los lados no paralelos del trapecio y son suplementarios, es decir, suman 180 grados.
P.8.- Según su posición en la circunferencia, algunos ángulos son ángulos central
Los ángulos son centrales porque están relacionados con el centro de la circunferencia. Un ángulo central es aquel que tiene su vértice en el centro de la circunferencia y sus lados son dos radios de la misma. Cuando trazamos una recta que une el centro de la circunferencia con los puntos finales de los radios que forman el ángulo, obtenemos una cuerda que divide la circunferencia en dos arcos. La medida del ángulo central es igual a la mitad de la medida del arco menor que se encuentra en su interior. Es decir, si denominamos "a" a la medida del arco menor, entonces la medida del ángulo central será "a/2". Los ángulos centrales son muy útiles en geometría ya que nos permiten relacionar las medidas de los ángulos con las medidas de los arcos que se encuentran en su interior. También son importantes en trigonometría, ya que los ángulos centrales son los que se utilizan para definir las funciones trigonométricas en la circunferencia unitaria Ejemplo: El ángulo semi-inscrito es aquel que tiene uno de sus lados que es un diámetro de la circunferencia y el otro lado es una cuerda. Este ángulo es de 90 grados.
P.8.1- Según su posición en la circunferencia, algunos ángulos son ángulos inscrito
Los ángulos inscritos son aquellos que tienen su vértice en la circunferencia y sus lados son dos cuerdas consecutivas. La medida de un ángulo inscrito es la mitad de la medida del arco que intercepta. Esto se puede demostrar utilizando la propiedad de que un ángulo inscrito que intercepta un arco es igual a la mitad de la medida del arco. Además, cualquier otro ángulo que intercepta el mismo arco tendrá la misma medida, lo que hace que los ángulos inscritos sean muy útiles en la geometría de la circunferencia. Ejemplo: Ángulo inscrito en un triángulo: En un triángulo inscrito en una circunferencia, los ángulos que forman los lados del triángulo con el arco opuesto son ángulos inscritos. Los tres ángulos inscritos de un triángulo inscrito en una circunferencia suman 180 grados.
P.8.2- Según su posición en la circunferencia, algunos ángulos son ángulos exinscrito.
Dividiendo el término en dos partes: "ex" y "inscrito". "Ex" significa "fuera" o "exterior", mientras que "inscrito" significa "escrito dentro de". Por lo tanto, los ángulos exinscritos se encuentran en el exterior de la circunferencia y no están inscritos en ella, pero están relacionados con la circunferencia. Los ángulos exinscritos se utilizan en muchos teoremas de geometría, como el teorema de Pitágoras y el teorema de Tales. Por ejemplo, en el teorema de Pitágoras, se utiliza el ángulo exinscrito para encontrar la longitud de la hipotenusa de un triángulo rectángulo. Además, en el teorema de Tales, los ángulos exinscritos se utilizan para demostrar que dos triángulos son semejantes.
P.8.3.- Según su posición en la circunferencia, algunos ángulos son ángulos interno.
Los ángulos internos se definen como aquellos que se encuentran dentro de una figura geométrica y cuyos lados están formados por dos segmentos de la misma. En el caso de una circunferencia, los ángulos internos se encuentran en su interior, es decir, entre dos radios o dos cuerdas de la circunferencia. La medida de los ángulos internos de una circunferencia está determinada por la longitud del arco que se forma entre los dos lados del ángulo y el radio de la circunferencia que lo contiene. Depende de su posición en la misma. Si el ángulo se encuentra en el centro de la circunferencia, entonces la medida del ángulo es igual a 360 grados, lo que equivale a la medida total de la circunferencia. Si el ángulo se encuentra en la periferia de la circunferencia, entonces su medida es igual a 180 grados, ya que se extiende a lo largo de la mitad de la circunferencia Ejemplo: Ángulos internos de un cuadrilátero, tiene cuatro ángulos internos. La suma de los ángulos internos de un cuadrilátero es siempre 360 grados.
P.8.4.- Según su posición en la circunferencia, algunos ángulos son externos.
Los ángulos externos se definen como aquellos que se encuentran fuera de una figura geométrica y cuyos lados están formados por una recta que intersecta a la figura misma. En el caso de una circunferencia, los ángulos externos se encuentran en su exterior, es decir, fuera de la circunferencia. La medida de los ángulos externos de una circunferencia está determinada por la longitud del arco que se forma entre el punto de intersección de la recta y la circunferencia y el radio de la circunferencia que lo contiene. En otras palabras, la medida de un ángulo externo en una circunferencia depende de su posición en la misma. Si la recta que intersecta a la circunferencia forma un ángulo recto con el radio que une el centro de la circunferencia con el punto de intersección, entonces el ángulo externo es igual a 90 grados. Si la recta intersecta a la circunferencia en dos puntos, entonces la medida del ángulo externo es igual a la mitad de la diferencia entre los ángulos centrales correspondientes. Ejemplo: Ángulos externos de un pentágono, tiene cinco ángulos externos. La suma de los ángulos externos de un pentágono es siempre 360 grados.
P.8.5.- Según su posición en la circunferencia, algunos ángulos son ángulos semi- inscrito.
Los ángulos semi-inscritos se definen como aquellos que se encuentran en la circunferencia y cuyos lados están formados por una recta que intersecta la circunferencia en un solo punto y por un diámetro que pasa por ese punto. Están formados por la mitad de un ángulo inscrito. La medida de los ángulos semi-inscritos de una circunferencia está determinada por la longitud del arco que se forma entre los dos lados del ángulo y la medida del diámetro de la circunferencia que lo contiene. En otras palabras, la medida de un ángulo semi-inscrito en una circunferencia depende de su posición en la misma. Si el ángulo semi-inscrito se encuentra en el centro de la circunferencia, entonces la medida del ángulo es igual a 90 grados, ya que se extiende a lo largo de la mitad de la circunferencia. Si el ángulo semi-inscrito se encuentra en cualquier otro punto de la circunferencia, su medida dependerá de la longitud del arco que se forma entre los dos lados del ángulo y la medida del diámetro de la circunferencia que lo contiene. Ejemplo: Ángulos semi-inscritos de una circunferencia, los ángulos semi-inscritos son aquellos que se forman entre una recta tangente y una recta secante que corta a la circunferencia en dos puntos. Estos ángulos tienen la mitad de medida que el ángulo central que subtiende el arco correspondiente.
P.9.- Según su lugar en un polígono, algunos ángulos son ángulos centrales.
Los ángulos centrales se definen como aquellos que tienen su vértice en el centro del polígono y cuyos lados están formados por dos lados consecutivos del polígono. En otras palabras, los ángulos centrales son aquellos que se extienden desde el centro del polígono hasta sus vértices. La medida de los ángulos centrales de un polígono está determinada por la cantidad de lados del polígono. Si el polígono tiene n lados, entonces la medida de cada ángulo central será igual a 360 grados dividido entre n. La posición de los ángulos centrales en un polígono es un factor importante para determinar su medida. Cada ángulo central está ubicado en el centro del polígono y se extiende hasta uno de sus vértices. Por lo tanto, la medida de cada ángulo central depende del número de lados del polígono y de la distancia desde el centro del polígono hasta su vértice. Ejemplo: Ángulo central en un triángulo, el ángulo central es aquel que se forma en el centro de la circunferencia circunscrita al triángulo. Este ángulo es igual a la medida del arco correspondiente y tiene como vértices el centro de la circunferencia y los vértices del triángulo.
P.9.1.- Según su lugar en un polígono, algunos ángulos son ángulos interiores.
Los ángulos interiores se definen como aquellos que se encuentran en el interior del polígono y cuyos lados son dos lados adyacentes del polígono. En otras palabras, los ángulos interiores son aquellos que se forman en la unión de dos lados consecutivos del polígono y que están en el interior del mismo. La medida de los ángulos interiores de un polígono está determinada por la cantidad de lados del polígono. Si el polígono tiene n lados, entonces la medida de cada ángulo interior será igual a 180 grados multiplicado por n-2 y dividido entre n. La posición de los ángulos interiores en un polígono es un factor importante para determinar su medida. Cada ángulo interior está ubicado en el interior del polígono y se forma en la unión de dos lados consecutivos del polígono. Por lo tanto, la medida de cada ángulo interior depende del número de lados del polígono y de la longitud de cada uno de los lados que forman el ángulo. Ejemplo: Ángulos interiores en un cuadrilátero, los ángulos interiores son aquellos que se forman en el interior del cuadrilátero cuando se unen dos lados consecutivos. La suma de los cuatro ángulos interiores de un cuadrilátero siempre es igual a 360 grados.
P.9.2- Según su lugar en un polígono, algunos ángulos son ángulos exterior
Los ángulos exteriores se definen como aquellos que se encuentran fuera del polígono y que se forman entre un lado del polígono y la prolongación del lado adyacente, se forman en la intersección de un lado del polígono con la prolongación del lado adyacente. La medida de los ángulos exteriores de un polígono está determinada por la cantidad de lados del polígono. Si el polígono tiene n lados, entonces la medida de cada ángulo exterior será igual a 360 grados dividido entre n. La posición de los ángulos exteriores en un polígono es un factor importante para determinar su medida. Cada ángulo exterior está ubicado fuera del polígono y se forma en la intersección de un lado del polígono con la prolongación del lado adyacente. Por lo tanto, la medida de cada ángulo exterior depende del número de lados del polígono y de la longitud de cada uno de los lados que forman el ángulo. Ejemplo: Ángulos exteriores de un triángulo, cada ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes a él. Por lo tanto, la suma de los tres ángulos exteriores de un triángulo siempre es igual a 360 grados.
Referencias
- Ángulos de la circunferencia. - Profesor de Dibujo. (2020, April). Profesor de Dibujo. https://www.profesordedibujo.com/geometria-plana/circunferencia/angulos-de-la-circunferencia/#:~:text=Se%20llama%20%C3%A1ngulo%20interior%20a,%C3%A1ngulo%20interior%20y%20su%20opuesto.
- Ángulos-Clasificación. (2023). Cecyt3.Ipn.mx. https://www.cecyt3.ipn.mx/ibiblioteca/mundodelasmatematicas/AngulosClasificacion.html#:~:text=1)%20%C3%81ngulo%20agudo%3A%20es%20aquel,aquel%20que%20mide%20180%C2%B0.
- Curvas abiertas y cerradas - Smartick. (2015, May 14). Smartick. https://www.smartick.es/blog/matematicas/geometria/curvas-abiertas-cerradas/
- Poligonales abiertas y cerradas - Smartick. (2015, May 22). Smartick. https://www.smartick.es/blog/matematicas/geometria/poligonales-abiertas-cerradas/ u/jennifer84. (2019, January 30). Clasificación de los Ángulos. GeoGebra. https://www.geogebra.org/m/rkcmeyyw#:~:text=Por%20suma%3A,que%20forman%20un%20%C3%A1ngulo%20per%C3%ADgono).
- Ángulos-Clasificación. (2023). Cecyt3.Ipn.mx. https://www.cecyt3.ipn.mx/ibiblioteca/mundodelasmatematicas/AngulosClasificacion.html#:~:text=Clasificaci%C3%B3n%20de%20%C3%A1ngulos%20seg%C3%BAn%20su%20medida&text=1)%20%C3%81ngulo%20agudo%3A%20es%20aquel,aquel%20que%20mide%20180%C2%B0.
- Alvarado, M. (2022, September 13). Tipos de ángulos - Plataforma Educativa Luca. Plataforma Educativa Luca: Curso En Línea Y Aprendizaje Esperado. https://www.lucaedu.com/tipos-de-angulos/#:~:text=Seg%C3%BAn%20su%20posici%C3%B3n%2C%20los%20%C3%A1ngulos,%C3%A1ngulo%20convexo%20y%20%C3%A1ngulo%20completo.
- SEP. (2022). Rectas paralelas y ángulos. Sep.gob.mx. https://nuevaescuelamexicana.sep.gob.mx/detalle-ficha/10961/
- Angulos en la circunferencia. (2022, March 30). Material Didáctico - Superprof; Material Didáctico - Superprof. https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/angulos-en-la-circunferencia.html#:~:text=El%20%C3%A1ngulo%20central%20tiene%20su,de%20su%20%C3%A1ngulo%20central%20correspondiente.&text=El%20%C3%A1ngulo%20inscrito%20tiene%20su,lados%20son%20secantes%20a%20ella.
- Clasificación de ángulos. (2022, April 27). Material Didáctico - Superprof; Material Didáctico - Superprof. https://www.superprof.es/apuntes/escolar/matematicas/geometria/basica/clasificacion-de-angulos.html