Diferencia entre revisiones de «Mentefacto Conceptual Números Racionales»
(Mnetefacto, Paquete, argumentaciones, referencias.) |
Sin resumen de edición |
||
| Línea 1: | Línea 1: | ||
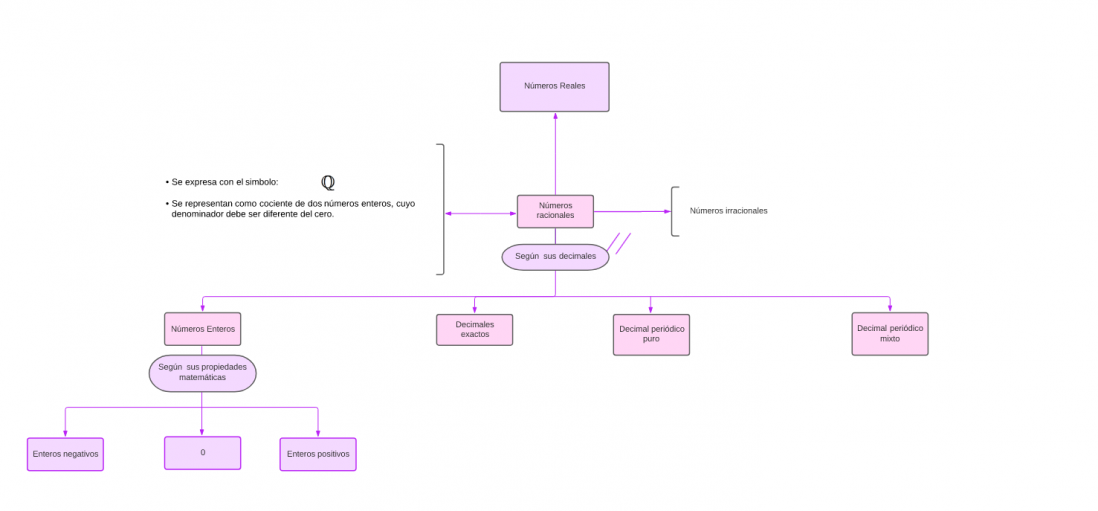
[[Archivo:Mentefacto Conceptual Numeros Racionales..png|centro|miniaturadeimagen|1098x1098px|Mentefacto Conceptual Números Racionales.]]<big>'''Paquete proposicional:'''</big> | |||
[[Archivo:Mentefacto Conceptual Numeros Racionales..png|centro|miniaturadeimagen|1098x1098px|Mentefacto Conceptual | |||
'''Supraordinada''' | |||
P1 Todo número racional es número real. | |||
'''Isoordinada''' | |||
P2.1. Todo número racional es el número expresado con el símbolo “[[Archivo:,.png|sinmarco]]”. | |||
P2.2. Todo número racional se representa como cociente de dos números enteros | |||
'''Exclusión''' | |||
P3. Ningún número racional es número irracional. | |||
'''Infraordinadas''' | |||
P4.1. Algún número racional según el tipo de fracción es aparente. | P4.1. Algún número racional según el tipo de fracción es aparente. | ||
P4.2. Algún número racional según el tipo de fracción es Propia. | P4.2. Algún número racional según el tipo de fracción es Propia. | ||
= | P4.3. Algún número racional según el tipo de fracción es Impropia. | ||
P1. Todo número racional es número real. | ----<gallery caption="Mentefactos Proposicionales"> | ||
Archivo:Ia.png|P1 Todo número racional es número real. | |||
Archivo:Aa.png|P2.1. Todo número racional es el número expresado con el símbolo “,.png”. | |||
Archivo:Aa.png|P2.2. Todo número racional se representa como cociente de dos números enteros | |||
Archivo:E.png|P3. Ningún número racional es número irracional. | |||
Archivo:Ai.png|P4.1. Algún número racional según el tipo de fracción es aparente. | |||
Archivo:Ai.png|P4.2. Algún número racional según el tipo de fracción es Propia. | |||
Archivo:Ai.png|P4.3. Algún número racional según el tipo de fracción es Impropia. | |||
</gallery> | |||
----<big>'''Argumentaciones'''</big> | |||
'''P1. Todo número racional es número real.''' | |||
Los números reales, son aquellos números que se los puede representar mediante una recta numérica, los cuales van a incluir a los números racionales e irracionales. | Los números reales, son aquellos números que se los puede representar mediante una recta numérica, los cuales van a incluir a los números racionales e irracionales. | ||
P2.1. Todo número racional es el número expresado con el símbolo “[[Archivo:,.png|sinmarco]]”. | '''P2.1. Todo número racional es el número expresado con el símbolo “[[Archivo:,.png|sinmarco]]”.''' | ||
Ya que está es la expresión abreviada matemática para representar este grupo de números, la cual significa cociente. | Ya que está es la expresión abreviada matemática para representar este grupo de números, la cual significa cociente. | ||
'''P2.2. Todo número racional se representa como cociente de dos números enteros .''' | |||
P2.2. Todo número racional se representa como cociente de dos números enteros . | |||
Porque estas se pueden representar mediante una fracción a/b, donde a y b son números enteros y además b es distinto de cero. | Porque estas se pueden representar mediante una fracción a/b, donde a y b son números enteros y además b es distinto de cero. | ||
P3. Ningún número racional es número irracional. | '''P3. Ningún número racional es número irracional.''' | ||
Porque los números racionales pueden ser expresados en forma de fracción o cociente de dos números mientras que los números irracionales sus decimales suelen ser infinitos, osea, no podemos representarlos en una fracción. | Porque los números racionales pueden ser expresados en forma de fracción o cociente de dos números mientras que los números irracionales sus decimales suelen ser infinitos, osea, no podemos representarlos en una fracción. | ||
P4.1. Algún número racional según el tipo de fracción es aparente. | '''P4.1. Algún número racional según el tipo de fracción es aparente.''' | ||
Son aquellas cuyo numerador es múltiplo del denominador. Si dividimos el numerador por el denominador obtenemos un número entero. | Son aquellas cuyo numerador es múltiplo del denominador. Si dividimos el numerador por el denominador obtenemos un número entero. | ||
P4.2. Algún número racional según el tipo de fracción es Propia. | '''P4.2. Algún número racional según el tipo de fracción es Propia.''' | ||
Son aquellas en las que el numerador es menor que el denominador; por lo tanto, son menores que la unidad. En la recta numérica se ubican entre el 0 y el 1. | Son aquellas en las que el numerador es menor que el denominador; por lo tanto, son menores que la unidad. En la recta numérica se ubican entre el 0 y el 1. | ||
P4.3. Algún número racional según el tipo de fracción es Impropia. | '''P4.3. Algún número racional según el tipo de fracción es Impropia.''' | ||
Son aquellas en las que el numerador es mayor que el denominador; por lo tanto, son mayores que la unidad. | Son aquellas en las que el numerador es mayor que el denominador; por lo tanto, son mayores que la unidad. | ||
----<big>'''Referencias Bibliográficas:'''</big> | |||
Números reales ¿Qué son? | Números reales ¿Qué son? | ||
Revisión actual - 17:39 27 jul 2023
Paquete proposicional:
Supraordinada
P1 Todo número racional es número real.
Isoordinada
P2.1. Todo número racional es el número expresado con el símbolo “
”.
P2.2. Todo número racional se representa como cociente de dos números enteros
Exclusión
P3. Ningún número racional es número irracional.
Infraordinadas
P4.1. Algún número racional según el tipo de fracción es aparente.
P4.2. Algún número racional según el tipo de fracción es Propia.
P4.3. Algún número racional según el tipo de fracción es Impropia.
- Mentefactos Proposicionales
P1 Todo número racional es número real.
P2.1. Todo número racional es el número expresado con el símbolo “,.png”.
P2.2. Todo número racional se representa como cociente de dos números enteros
P3. Ningún número racional es número irracional.
P4.1. Algún número racional según el tipo de fracción es aparente.
P4.2. Algún número racional según el tipo de fracción es Propia.
P4.3. Algún número racional según el tipo de fracción es Impropia.
Argumentaciones
P1. Todo número racional es número real.
Los números reales, son aquellos números que se los puede representar mediante una recta numérica, los cuales van a incluir a los números racionales e irracionales.
P2.1. Todo número racional es el número expresado con el símbolo “”.
Ya que está es la expresión abreviada matemática para representar este grupo de números, la cual significa cociente.
P2.2. Todo número racional se representa como cociente de dos números enteros .
Porque estas se pueden representar mediante una fracción a/b, donde a y b son números enteros y además b es distinto de cero.
P3. Ningún número racional es número irracional.
Porque los números racionales pueden ser expresados en forma de fracción o cociente de dos números mientras que los números irracionales sus decimales suelen ser infinitos, osea, no podemos representarlos en una fracción.
P4.1. Algún número racional según el tipo de fracción es aparente.
Son aquellas cuyo numerador es múltiplo del denominador. Si dividimos el numerador por el denominador obtenemos un número entero.
P4.2. Algún número racional según el tipo de fracción es Propia.
Son aquellas en las que el numerador es menor que el denominador; por lo tanto, son menores que la unidad. En la recta numérica se ubican entre el 0 y el 1.
P4.3. Algún número racional según el tipo de fracción es Impropia.
Son aquellas en las que el numerador es mayor que el denominador; por lo tanto, son mayores que la unidad.
Referencias Bibliográficas:
Números reales ¿Qué son?
By Software DELSOL Container: Sdelsol.com Year: 2020 URL: https://www.sdelsol.com/glosario/numeros-reales/#:~:text=utilizando%20n%C3%BAmeros%20reales.-,Qu%C3%A9%20son%20los%20n%C3%BAmeros%20reales,menos%20infinito%20y%20m%C3%A1s%20infinito.
Conoce los números racionales y sus propiedades
By Container: Smartick Year: 2018 URL: https://www.smartick.es/blog/matematicas/numeros-enteros/numeros-racionales-propiedades/#:~:text=Propiedades%20de%20n%C3%BAmeros%20racionales,b%20es%20distinto%20de%20cero
Conoce los números racionales y sus propiedades
By Container: Smartick Year: 2018 URL: https://www.smartick.es/blog/matematicas/numeros-enteros/numeros-racionales-propiedades
Números irracionales: qué son, cuáles son y ejemplos
By Toda Materia Container: Toda Materia Publisher: Toda Materia Year: 2021 URL: https://www.todamateria.com/numeros-irracionales/
Números irracionales: qué son, cuáles son y ejemplos
By Toda Materia Container: Toda Materia Publisher: Toda Materia Year: 2021 URL: https://www.todamateria.com/numeros-irracionales/
Tipos de fracciones | Fracciones equivalentes
By Silvana Realini Cujó Container: Ceiploreto.es Year: 2023 URL: http://www.ceiploreto.es/sugerencias/ceibal/Fracciones_equivalentes/tipos_de_fracciones.html#:~:text=Fracciones%20aparentes%3A%20son%20aquellas%20cuyo,50%2F10%2C%20…