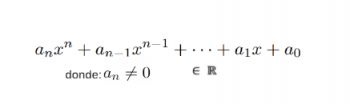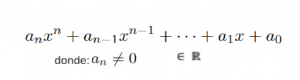Mentefacto Sistema de Ecuaciones Polinómicas

Mentefacto

Mentefacto Sistema De Ecuaciones Polinómicas

Paquete proposicional:

P1) Todo sistema de ecuaciones polinómicas es un sistema de ecuaciones.

P2.1) Todo sistema de ecuaciones polinómicas Tienen dos o más ecuaciones del tipo

P2.2) Todo sistema de ecuaciones polinómicas se resuelve por métodos (Sustitucion, igualacion, graficación)

P3.1) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones trigonométricas.

P3.2) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones exponenciales.

P3.3) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones logarítmicas.

P4.1.1) Algún sistema de Ecuaciones polinómicas  según el grado de la variable directriz  es de 1er grado (Lineal)

P4.1.2) Algún sistema de Ecuaciones polinómicas según el grado de la variable directriz es de 2do grado (Cuadrática)

P4.1.3) Algún sistema de Ecuaciones polinómicas según el grado de la variable directriz es de grado superior (General)

P4.2.1) Algún sistema de ecuaciones polinómicas según el número de soluciones es compatible

P4.2.1.1) Algunos sistemas de ecuaciones polinómicas según su número de soluciones son compatibles determinados.

P4.2.1.2) Algunos sistemas de ecuaciones polinómicas según su número de soluciones son compatibles indeterminados.

P4.2.2) Algún sistema de ecuaciones polinómicas según el número de soluciones es incompatible.

Análisis proposicional:

P1) Todo sistema de ecuaciones polinómicas es un sistema de ecuaciones.

Analisis Proposicional Sistema de Ecuaciones Polinomicas P1)

P2.1) Todo sistema de ecuaciones polinómicas Tienen dos o más ecuaciones del tipo

Análisis Proposicional Sistema de Ecuaciones Polinómicas P2.1)

P2.2) Todo sistema de ecuaciones polinómicas se resuelve por métodos (Sustitucion, igualacion, graficación)

Análisis Proposicional Sistema de Ecuaciones Polinómicas P2.2)

P3.1) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones trigonométricas.

Análisis Proposicional Sistema de Ecuaciones Polinómicas P3.1)

P3.2) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones exponenciales.

Análisis Proposicional Sistema de Ecuaciones Polinómicas P3.2)

P3.3) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones logarítmicas.

Análisis Proposicional Sistema de Ecuaciones Polinómicas P3.3)

P4.1.1) Algún sistema de Ecuaciones polinómicas  según el grado de la variable directriz  es de 1er grado (Lineal)

Análisis Proposicional Sistema de Ecuaciones Polinómicas P4.1.1)

P4.1.2) Algún sistema de Ecuaciones polinómicas según el grado de la variable directriz es de 2do grado (Cuadrática)

Análisis Proposicional Sistema de Ecuaciones Polinómicas P4.1.2)

P4.1.3) Algún sistema de Ecuaciones polinómicas según el grado de la variable directriz es de grado superior (General)

Análisis Proposicional Sistema de Ecuaciones Polinómicas P4.1.3)

P4.2.1) Algún sistema de ecuaciones polinómicas según el número de soluciones es compatible

Análisis Proposicional Sistema de Ecuaciones Polinómicas P4.2.1)

P4.2.1.1) Algunos sistemas de ecuaciones polinómicas según su número de soluciones son compatibles determinados.

Análisis Proposicional Sistema de Ecuaciones Polinómicas P4.2.1.1)

P4.2.1.2) Algunos sistemas de ecuaciones polinómicas según su número de soluciones son compatibles indeterminados.

Análisis Proposicional Sistema de Ecuaciones Polinómicas P4.2.1.2)

P4.2.2) Algún sistema de ecuaciones polinómicas según el número de soluciones es incompatible.

Análisis Proposicional Sistema de Ecuaciones Polinómicas P4.2.2)

Argumentaciones:

P1) Todo sistema de ecuaciones polinómicas es un sistema de ecuaciones.

Argumentación: Una ecuación polinómica es una expresión algebraica que contiene uno o más términos que involucran una variable elevada a un exponente entero no negativo. Un sistema de ecuaciones polinómicas es un conjunto de dos o más ecuaciones polinómicas que involucran las mismas variables. Como un sistema de ecuaciones polinómicas es una colección de ecuaciones, entonces es, por definición, un sistema de ecuaciones.

P2.1) Todo sistema de ecuaciones polinómicas Tienen dos o más ecuaciones del tipo

Argumentación: Una ecuación polinómica es una expresión algebraica que contiene uno o más términos que involucran una variable elevada a un exponente entero no negativo. Un sistema de ecuaciones polinómicas es un conjunto de dos o más ecuaciones polinómicas que involucran las mismas variables. Por lo tanto, todo sistema de ecuaciones polinómicas debe tener al menos dos ecuaciones del tipo polinómico.

P2.2) Todo sistema de ecuaciones polinómicas utiliza métodos de resolución (Sustitucion, igualacion, graficación)

Argumentación: Para resolver un sistema de ecuaciones polinómicas, se utilizan varios métodos, como sustitución, igualación y graficación. Por lo tanto, todo sistema de ecuaciones polinómicas utiliza al menos uno de estos métodos para encontrar las soluciones.

Ejemplo:

Resolviendo un sistema de ecuaciones polinómicas por sustitución

Considere el siguiente sistema de ecuaciones polinómicas:

x + y = 5

x - y = 1

x = 5 - y

5 - y - y = 1

x + 2 = 5

lo que nos da x = 3. Por lo tanto, la solución del sistema es x = 3 e y = 2.

Resolviendo un sistema de ecuaciones polinómicas por igualación

Considere el siguiente sistema de ecuaciones polinómicas:

2x + 3y = 13

4x - 5y = -2

x = (13 - 3y) / 2

x = (5y - 2) / 4

(13 - 3y) / 2 = (5y - 2) / 4

Resolviendo esta ecuación, obtenemos y = 1.

Luego podemos sustituir este valor de y en cualquiera de las dos ecuaciones originales para encontrar x:

2x + 3(1) = 13

lo que nos da x = 5. Por lo tanto, la solución del sistema es x = 5 e y = 1.

Resolviendo un sistema de ecuaciones polinómicas por gráficos

Considere el siguiente sistema de ecuaciones polinómicas:

y = x^2 - 4

y = -2x + 1

Para resolver este sistema por gráficos, podemos graficar ambas ecuaciones en el mismo plano cartesiano y encontrar los puntos de intersección.

intersectan en dos puntos, uno en aproximadamente (-1.6, 6.6) y otro en aproximadamente (1.6, -1.6). Por lo tanto, la solución del sistema es x = -1.6 e y = 6.6, o x = 1.6  e  y = -1.6.

P3.1) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones trigonométricas.

Argumentación: Las ecuaciones trigonométricas involucran funciones trigonométricas, como seno, coseno y tangente. Las ecuaciones polinómicas no contienen términos trigonométricos, por lo que ningún sistema de ecuaciones polinómicas puede ser un sistema de ecuaciones trigonométricas.

P3.2) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones exponenciales.

Argumentación: Las ecuaciones exponenciales involucran una variable en el exponente de una base constante. Las ecuaciones polinómicas no contienen términos exponenciales, por lo que ningún sistema de ecuaciones polinómicas puede ser un sistema de ecuaciones exponenciales.

P3.3) Ningún sistema de Ecuaciones polinómicas es un sistema de ecuaciones logarítmicas.

Argumentación: Las ecuaciones logarítmicas involucran el logaritmo de una variable. Las ecuaciones polinómicas no contienen términos logarítmicos, por lo que ningún sistema de ecuaciones polinómicas puede ser un sistema de ecuaciones logarítmicas.

P4.1.1) Algún sistema de Ecuaciones polinómicas  según el grado de la variable directriz  es de 1er grado (Lineal)

Argumentación: Una ecuación polinómica de primer grado se representa como ax + b = 0, donde a y b son constantes y x es una variable. Un sistema de ecuaciones polinómicas puede contener varias ecuaciones de primer grado en una o más variables, lo que significa

P4.1.2) Algún sistema de Ecuaciones polinómicas según el grado de la variable directriz es de 2do grado (Cuadrática)

Argumentación: Una ecuación polinómica de segundo grado se define como una ecuación de la forma ax^2 + bx + c = 0, donde a, b y c son constantes y a ≠ 0. Un sistema de ecuaciones polinómicas que contiene una o más ecuaciones de segundo grado también se conoce como un sistema de ecuaciones polinómicas de segundo grado o un sistema de ecuaciones cuadráticas. Por lo tanto, existe al menos un sistema de ecuaciones polinómicas que es de segundo grado.

P4.1.3) Algún sistema de Ecuaciones polinómicas según el grado de la variable directriz es de grado superior (General)

Argumentación: Toda ecuación polinómica se puede escribir como una suma de términos de la forma ax^n, donde a es una constante y n es el grado de la variable directriz. Por lo tanto, un sistema de ecuaciones polinómicas de grado superior se puede definir como un sistema de ecuaciones que contiene al menos una ecuación con un grado mayor que 2. Dado que existen ecuaciones polinómicas de cualquier grado, se sigue que también existen sistemas de ecuaciones polinómicas de grado superior.

P4.2.1) Algún sistema de ecuaciones polinómicas según el número de soluciones es compatible

Argumentación : Un sistema de ecuaciones polinómicas es compatible si tiene una o más soluciones, es decir, hay valores de las variables que satisfacen simultáneamente todas las ecuaciones del sistema. Dado que hay sistemas de ecuaciones polinómicas que tienen soluciones, existe al menos un sistema de ecuaciones polinómicas que es compatible.

P4.2.1.1) Algunos sistemas de ecuaciones polinómicas según su número de soluciones son compatibles determinados.

Argumentación: Un sistema de ecuaciones polinómicas es compatible determinado si tiene una única solución. Por lo tanto, existen sistemas de ecuaciones polinómicas que tienen exactamente una solución, lo que significa que hay algunos sistemas de ecuaciones polinómicas que son compatibles determinados.

P4.2.1.2) Algunos sistemas de ecuaciones polinómicas según su número de soluciones son compatibles indeterminados.

Argumentación: Un sistema de ecuaciones polinómicas es compatible indeterminado si tiene más de una solución posible. Por lo tanto, existen sistemas de ecuaciones polinómicas que tienen más de una solución, lo que significa que hay algunos sistemas de ecuaciones polinómicas que son compatibles indeterminados.

P4.2.2)  Algún sistema de ecuaciones polinómicas según el número de soluciones es incompatible.

Argumentación: Un sistema de ecuaciones polinómicas es incompatible si no tiene solución. Dado que hay sistemas de ecuaciones polinómicas que no tienen solución, existe al menos un sistema de ecuaciones polinómicas que es incompatible.

Referencias Bibliográficas :

1. Isoordinadas https://www.ehu.eus/~mtpalezp/descargas/olimpoli.pdf
2. System of Linear Equations (Simultaneous Equations) | Brilliant Math & Science Wiki. (2023). Brilliant.org. https://brilliant.org/wiki/system-of-linear-equations/#systems-of-equation‌
3. Vigneron, A., Dpto, T., & De Matemáticas. (n.d.). Sistemas polinomiales: introducción y aplicaciones. https://ocw.uca.es/pluginfile.php/124/mod_resource/content/1/introduccion_polinomiales.pdf
4. ‌Ecuaciones polinómicas: qué son, tipos, ejemplos, ejercicios. (2021, July 14). Lifeder. https://www.lifeder.com/ecuaciones-polinomicas/
5. ‌Ecuaciones e inecuaciones de Primer Grado con una incógnita. (n.d.). https://asuarez.files.wordpress.com/2008/10/ecuaciones.pdf
6. ‌yosoytuprofe. (2018, June 11). Sistemas de ecuaciones de segundo grado - Yo Soy Tu Profe. Yo Soy Tu Profe. https://yosoytuprofe.20minutos.es/2018/06/11/sistemas-de-ecuaciones-de-segundo-grado/
7. ‌de, C. (2007, December 25). término matemático. Wikipedia.org; Wikimedia Foundation, Inc. https://es.wikipedia.org/wiki/Ecuaci%C3%B3n_algebraica
8. ‌Ecuaciones polinómicas de grado superior a dos. (2018, November 8). MÁS MATES .net; MÁS MATES .net. https://masmates.net/2018/11/08/ecuaciones-polinomicas-de-grado-superior-a-dos/
9. ‌Ecuaciones de grado superior a dos. Bicuadradas y tricuadradas. (2016). Laescuelaencasa.com. https://laescuelaencasa.com/matematicas-2/ecuaciones/clase-4-ecuaciones-grado-superior-dos/
10. ‌de, C. (2006, December 15). Sistema de ecuaciones algebraicas. Wikipedia.org; Wikimedia Foundation, Inc. https://es.wikipedia.org/wiki/Sistema_de_ecuaciones_algebraicas
11. ‌https://www.facebook.com/udoenews. (2023, January 7). ¿Qué es una Ecuación Incompatible? - UDOE. UDOE. https://udoe.es/que-es-una-ecuacion-incompatible/
12. ‌Sistemas de ecuaciones compatibles e incompatibles condiciones. (2014). Slideshare.net. https://es.slideshare.net/HumbertoNuez1/sistemas-de-ecuaciones-compatibles-e-incompatibles-condiciones