Diferencia entre revisiones de «Pseudomentefacto de números dígitos»
(Pseudomentefacto números dígitos) |
|||
| Línea 16: | Línea 16: | ||
P3.2 Algunos números dígitos son números pares | P3.2 Algunos números dígitos son números pares | ||
====== Exclusiones ====== | ====== Exclusiones ====== | ||
| Línea 27: | Línea 25: | ||
=== Mentefactos === | === Mentefactos === | ||
<gallery> | |||
Archivo:Mentefacto A.png|P1.1 Todos los números dígitos son números naturales. | |||
Archivo:Mentefacto A.png|P2.1 Todos los números dígitos son números de una sola cifra. | |||
Archivo:Mentefacto A.png|P2.2 Todos los números dígitos son números positivos. | |||
Archivo:Mentefacto I.png|P3. 1 Algunos números dígitos son números impares. | |||
Archivo:Mentefacto Tipo I 1.jpeg|P3.2 Algunos números dígitos son números pares | |||
Archivo:Mentefacto tipoe.png|P4. 1 Ningunos números dígitos son números polidígitos. | |||
Archivo:Mentefacto tipoe.png|P4.2 Ningunos números dígitos son negativos | |||
</gallery> | |||
---- | ---- | ||
| Línea 36: | Línea 41: | ||
====== Argumentación ====== | ====== Argumentación ====== | ||
Todos los números dígitos son números naturales porque son números que son enteros, racionales, reales. | Todos los números dígitos son números naturales porque son números que son enteros, racionales, reales. | ||
P2.1 Todos los números dígitos son números de una sola cifra. | |||
P2.1 Todos los números dígitos son números de una sola cifra. | P2.1 Todos los números dígitos son números de una sola cifra. | ||
| Línea 41: | Línea 47: | ||
====== Argumentación ====== | ====== Argumentación ====== | ||
Porque son números únicos y originan a los demás números además que son positivos | Porque son números únicos y originan a los demás números además que son positivos | ||
P2.2 Todos los números dígitos son números positivos. | |||
P2.2 Todos los números dígitos son números positivos. | P2.2 Todos los números dígitos son números positivos. | ||
| Línea 46: | Línea 53: | ||
====== Argumentación ====== | ====== Argumentación ====== | ||
Porque todo número natural es positivo | Porque todo número natural es positivo | ||
P3. 1 Algunos números dígitos son números impares. | |||
P3. 1 Algunos números dígitos son números impares. | P3. 1 Algunos números dígitos son números impares. | ||
| Línea 51: | Línea 59: | ||
====== Argumentación ====== | ====== Argumentación ====== | ||
Porque algunos números dígitos no son múltiplos de dos | Porque algunos números dígitos no son múltiplos de dos | ||
P3.2 Algunos números dígitos son números pares | |||
P3.2 Algunos números dígitos son números pares | P3.2 Algunos números dígitos son números pares | ||
| Línea 56: | Línea 65: | ||
====== Argumentación ====== | ====== Argumentación ====== | ||
Porque algunos números dígitos son múltiplos de 2 | Porque algunos números dígitos son múltiplos de 2 | ||
P4.1 Ningunos números dígitos son números polidígitos. | |||
P4.1 Ningunos números dígitos son números polidígitos. | P4.1 Ningunos números dígitos son números polidígitos. | ||
| Línea 61: | Línea 71: | ||
====== Argumentación ====== | ====== Argumentación ====== | ||
Porque son números únicos que originan a los demás números | Porque son números únicos que originan a los demás números | ||
P4.2 Ningunos números dígitos son negativos | |||
P4.2 Ningunos números dígitos son negativos | P4.2 Ningunos números dígitos son negativos | ||
| Línea 66: | Línea 77: | ||
====== Argumentación ====== | ====== Argumentación ====== | ||
Porque los números dígitos son números naturales | Porque los números dígitos son números naturales | ||
---- | |||
=== Referencias === | |||
“Valor Posicional Y Nombres de Los Números Enteros.” [https://content.nroc.org/DevelopmentalMath.HTML5/U01L1T1/TopicText/es/textbook.html#:~:text=El%20sistema%20num%C3%A9rico ''Content.nroc.org'', content.nroc.org/DevelopmentalMath.HTML5/U01L1T1/TopicText/es/textbook.html#:~:text=El%20sistema%20num%C3%A9rico. Accessed 20 Apr. 2023.] | |||
Westreicher, Guillermo. “Dígito.” [https://economipedia.com/definiciones/digito.html ''Economipedia'', economipedia.com/definiciones/digito.html. Accessed 20 Apr. 2023.] | |||
---- | ---- | ||
Revisión actual - 00:03 21 abr 2023
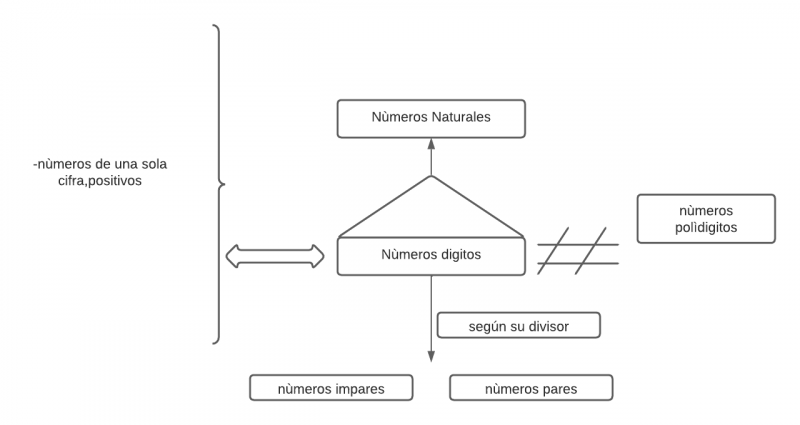
Paquete Proposicional
Supraordinada
P1.1 Todos los números dígitos son números naturales.
Isoordinadas
P2.1 Todos los números dígitos son números de una sola cifra.
P2.2 Todos los números dígitos son números positivos.
Infraordinadas
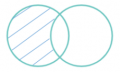
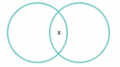
P3. 1 Algunos números dígitos son números impares.
P3.2 Algunos números dígitos son números pares
Exclusiones
P4. 1 Ningunos números dígitos son números polidígitos.
P4.2 Ningunos números dígitos son negativos
Mentefactos
P1.1 Todos los números dígitos son números naturales.
P2.1 Todos los números dígitos son números de una sola cifra.
P2.2 Todos los números dígitos son números positivos.
P3. 1 Algunos números dígitos son números impares.
P3.2 Algunos números dígitos son números pares
P4. 1 Ningunos números dígitos son números polidígitos.
P4.2 Ningunos números dígitos son negativos
Argumentaciones
P1.1 Todos los números dígitos son números naturales.
Argumentación
Todos los números dígitos son números naturales porque son números que son enteros, racionales, reales. P2.1 Todos los números dígitos son números de una sola cifra.
P2.1 Todos los números dígitos son números de una sola cifra.
Argumentación
Porque son números únicos y originan a los demás números además que son positivos P2.2 Todos los números dígitos son números positivos.
P2.2 Todos los números dígitos son números positivos.
Argumentación
Porque todo número natural es positivo P3. 1 Algunos números dígitos son números impares.
P3. 1 Algunos números dígitos son números impares.
Argumentación
Porque algunos números dígitos no son múltiplos de dos P3.2 Algunos números dígitos son números pares
P3.2 Algunos números dígitos son números pares
Argumentación
Porque algunos números dígitos son múltiplos de 2 P4.1 Ningunos números dígitos son números polidígitos.
P4.1 Ningunos números dígitos son números polidígitos.
Argumentación
Porque son números únicos que originan a los demás números P4.2 Ningunos números dígitos son negativos
P4.2 Ningunos números dígitos son negativos
Argumentación
Porque los números dígitos son números naturales
Referencias
“Valor Posicional Y Nombres de Los Números Enteros.” Content.nroc.org, content.nroc.org/DevelopmentalMath.HTML5/U01L1T1/TopicText/es/textbook.html#:~:text=El%20sistema%20num%C3%A9rico. Accessed 20 Apr. 2023.
Westreicher, Guillermo. “Dígito.” Economipedia, economipedia.com/definiciones/digito.html. Accessed 20 Apr. 2023.