Diferencia entre revisiones de «Pseudomentefacto Par Ordenado»
(Arreglo Fuentes) |
(Pseudomentefacto) |
||
| Línea 1: | Línea 1: | ||
[[Archivo:Pseudomentefacto Par Ordenado.png|centro|miniaturadeimagen|731x731px|Pseudomentefacto Par Ordenado]] | [[Archivo:Pseudomentefacto Par Ordenado 1.png|centro|miniaturadeimagen|731x731px|Pseudomentefacto Par Ordenado]] | ||
----'''Supraordinadas''' | ----'''Supraordinadas''' | ||
Revisión actual - 22:45 20 abr 2023
Supraordinadas
P1. Todo Par Ordenado es un Objeto Matematico.
Isoordinadas
P2.1: Todo Par Ordenado es un Objeto Matematico que distinge un elemento del otro (x,y).
P2.2: Todo Par Ordenado es un Objeto Matematico que Indica una posicion de un punto en el plano cartesiano.
Exclusiones
P3.1: Ningun Par Ordenado es Funcion.
P3.2: Ningun Par Ordenado es Conjunto.
- Mentefactos proposicionales
P1: Todo Par Ordenado es un Objeto Matematico.
P2.1: Todo Par Ordenado es un Objeto Matematico que distinge un elemento del otro (x,y).
P2.2: Todo Par Ordenado es un Objeto Matematico que Indica una posicion de un punto en el plano cartesiano.
P3.1: Ningun Par Ordenado es Funcion.
P3.2: Ningun Par Ordenado es Conjunto.
Argumentaciones
P1. Todo Par Ordenado es un Objeto Matematico.
El par ordenado se caracteriza por organizar dos objetos matematicos en el que se distinge un elemento del otro.
(x,y)
P2.1: Todo Par Ordenado es un Objeto Matematico que distinge un elemento del otro (x,y).
Ya que el par ordenado organiza estos dos elementos de una forme que se distingue de otro orden pero con los mismo elementos, esto nos dice que no es lo mismo (x,y) que (y,x) ya que puede que sean los mismo elementos pero con diferente orden y si lo representamos en un plano cartesiano serian dos puntos diferentes.
P2.2: Todo Par Ordenado es un Objeto Matematico que Indica una posicion de un punto en el plano cartesiano.
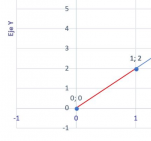
Ya que si tenemos dos numeron podemos representar uno en el eje X, otro en el eje Y, y conseguir un punto en el plano cartesiano como ejemplo:
En esta imagen podemos ver que tenemos un par ordenado de (1,2) donde 1 esta en el eje X y 2 en el eje Y.
P3.1: Ningun Par Ordenado es Funcion.
El par ordenado no es funcion ya que sus elementos no dependen, ni tienen relacion con otros, estos pueden ser representados sin la nesecidad de otro.
P3.2: Ningun Par Ordenado es Conjunto.
El par ordenado no es conjunto ya que solo agrupa datos para representarlos en un plano cartesiano, no hace que estos dos pertenezcan a un mismo grupo.
Referencias
- (Martes, 29 de septiembre del 2020), https://ciencias-basicas.com/matematica/superior/relaciones-matematicas/par-ordenado/
- White Tiger, (Martes, 23 de octubre de 2012), http://parordenadoicss.blogspot.com/2012/10/en-matematicas-un-par-ordenado-una.html
- Pérez Porto, J., Gardey, A. (26 de diciembre de 2017). Función matemática - Qué es, definición, funciones y ejemplos. Definicion.de. Última actualización el 12 de abril de 2021. Recuperado el 15 de abril de 2023 de https://definicion.de/funcion-matematica/
- Superprof, (Martes, 4 de agosto del 2020), https://www.superprof.es/apuntes/escolar/matematicas/calculo/funciones/concepto-de-funcion.html