Diferencia entre revisiones de «Pseudomentefacto Unidades de Mil»
(Correcion del mentefacto) |
(Correccion del paquete proposicional) |
||
| Línea 32: | Línea 32: | ||
----'''<big>Argumentaciones</big>''' | ----'''<big>Argumentaciones</big>''' | ||
'''P1. | '''P1.Toda unidad de mil es número entero.''' | ||
Argumentación: Los números enteros son un conjunto de números que incluyen todos los números negativos, el cero y todos los números positivos que no tienen decimales y fracciones. Se representan con el símbolo "Z" y se expresan como una secuencia infinita de números: ..., -3, -2, -1, 0, 1, 2, 3, ... | Argumentación: Los números enteros son un conjunto de números que incluyen todos los números negativos, el cero y todos los números positivos que no tienen decimales y fracciones. Se representan con el símbolo "Z" y se expresan como una secuencia infinita de números: ..., -3, -2, -1, 0, 1, 2, 3, ... | ||
'''P2.1 | '''P2.1 Toda unidad de mil es número que utiliza 4 cifras.''' | ||
Argumentación: Las cifras en los números definirán la cantidad de un número, puede ir en centenas o decenas, y en la unidad de mil se utilizan 4 cifras para que puedan ser contados de mil en mil. | Argumentación: Las cifras en los números definirán la cantidad de un número, puede ir en centenas o decenas, y en la unidad de mil se utilizan 4 cifras para que puedan ser contados de mil en mil. | ||
'''P2.2 | '''P2.2 Toda unidad de mil es numero que se cuenta de mil en mil.''' | ||
Argumentación: Como su nombre dice, son unidades de mil las cuales se van contando de mil en mil, siendo como ejemplo 1000, 2000, 3000…Entre más números que se cuenten. | Argumentación: Como su nombre dice, son unidades de mil las cuales se van contando de mil en mil, siendo como ejemplo 1000, 2000, 3000…Entre más números que se cuenten. | ||
'''P3.1 | '''P3.1 Ninguna unidad de mil es número con decenas.''' | ||
Argumentación: Estas no tienen las mismas cifras, son menores a las cifras que poseen las unidades de mil, ya que las decenas ocupan la segunda cifra desde la derecha. 10 unidades son una decena. | Argumentación: Estas no tienen las mismas cifras, son menores a las cifras que poseen las unidades de mil, ya que las decenas ocupan la segunda cifra desde la derecha. 10 unidades son una decena. | ||
'''P3.2 | '''P3.2 Ninguna unidad de mil es número con centenas.''' | ||
Argumentación: A diferencia a los números con unidades de mil, las centenas ocupan la tercera columna comenzando por la derecha. | Argumentación: A diferencia a los números con unidades de mil, las centenas ocupan la tercera columna comenzando por la derecha. | ||
'''P3. | '''P3.3Ninguna unidad de mil es número decimal.''' | ||
Argumentación: Un número decimal es un número no entero, compuesto por una parte entera y una parte decimal, se usan cuando queremos representar números que son más pequeños que la unidad. Por ejemplo, 0,5 es un número decimal, y es más pequeño que la unidad, se cumple que 1 es mayor que 0,5. | Argumentación: Un número decimal es un número no entero, compuesto por una parte entera y una parte decimal, se usan cuando queremos representar números que son más pequeños que la unidad. Por ejemplo, 0,5 es un número decimal, y es más pequeño que la unidad, se cumple que 1 es mayor que 0,5. | ||
'''P4.1 | '''P4.1 Alguna unidad de mil es número par.''' | ||
Argumentación: Cualquier número que sea número natural puede ser par o impar. Par implica que se pueda dividir en la mitad y que sea un número exacto. | Argumentación: Cualquier número que sea número natural puede ser par o impar. Par implica que se pueda dividir en la mitad y que sea un número exacto. | ||
'''P4.2 | '''P4.2 Alguna unidad de mil es número impares.''' | ||
Argumentación: Los números que sean naturales pueden ser pares o impares y los impares implican que no contienen una mitad exacta y son divisiones inexactas. | Argumentación: Los números que sean naturales pueden ser pares o impares y los impares implican que no contienen una mitad exacta y son divisiones inexactas. | ||
Revisión del 22:11 21 abr 2023
Paquete Proposicional
Supraordinada
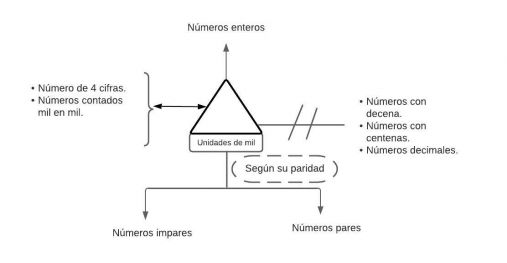
P1. Toda unidad de mil es número entero.
Isoordinada
P2.1 Toda unidad de mil es número que utiliza 4 cifras.
P2.2 Toda unidad de mil es numero que se cuenta de mil en mil.
Exclusión
P3.1 Ninguna unidad de mil es número con decenas.
P3.2 Ninguna unidad de mil es número con centenas.
P3.3Ninguna unidad de mil es número decimal.
Infraordinadas
P4.1 Alguna unidad de mil es número par.
P4.2 Alguna unidad de mil es número impares.
Mentefactos proposicionales
Argumentaciones
P1.Toda unidad de mil es número entero.
Argumentación: Los números enteros son un conjunto de números que incluyen todos los números negativos, el cero y todos los números positivos que no tienen decimales y fracciones. Se representan con el símbolo "Z" y se expresan como una secuencia infinita de números: ..., -3, -2, -1, 0, 1, 2, 3, ...
P2.1 Toda unidad de mil es número que utiliza 4 cifras.
Argumentación: Las cifras en los números definirán la cantidad de un número, puede ir en centenas o decenas, y en la unidad de mil se utilizan 4 cifras para que puedan ser contados de mil en mil.
P2.2 Toda unidad de mil es numero que se cuenta de mil en mil.
Argumentación: Como su nombre dice, son unidades de mil las cuales se van contando de mil en mil, siendo como ejemplo 1000, 2000, 3000…Entre más números que se cuenten.
P3.1 Ninguna unidad de mil es número con decenas.
Argumentación: Estas no tienen las mismas cifras, son menores a las cifras que poseen las unidades de mil, ya que las decenas ocupan la segunda cifra desde la derecha. 10 unidades son una decena.
P3.2 Ninguna unidad de mil es número con centenas.
Argumentación: A diferencia a los números con unidades de mil, las centenas ocupan la tercera columna comenzando por la derecha.
P3.3Ninguna unidad de mil es número decimal.
Argumentación: Un número decimal es un número no entero, compuesto por una parte entera y una parte decimal, se usan cuando queremos representar números que son más pequeños que la unidad. Por ejemplo, 0,5 es un número decimal, y es más pequeño que la unidad, se cumple que 1 es mayor que 0,5.
P4.1 Alguna unidad de mil es número par.
Argumentación: Cualquier número que sea número natural puede ser par o impar. Par implica que se pueda dividir en la mitad y que sea un número exacto.
P4.2 Alguna unidad de mil es número impares.
Argumentación: Los números que sean naturales pueden ser pares o impares y los impares implican que no contienen una mitad exacta y son divisiones inexactas.
Referencias
Los números: Valor posicional. (n.d.). GCFGlobal.org. Retrieved April 21, 2023, from
https://edu.gcfglobal.org/es/los-numeros/valor-posicional/1/
Primaria, M. (n.d.). Las unidades de millar. Mundo Primaria.
https://www.mundoprimaria.com/recursos-matematicas/las-unidades-de-millar
UNIDADES, DECENAS Y CENTENAS ® Qué son + Ejercicios en PDF. (n.d.). Juegos Infantiles. Retrieved April 21, 2023, from
https://juegosinfantiles.bosquedefantasias.com/matematicas/unidades-decenas-centenas