Diferencia entre revisiones de «Mentefacto Álgebra de Conjuntos»
m (Corrección texto) |
Sin resumen de edición |
||
| (No se muestran 2 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
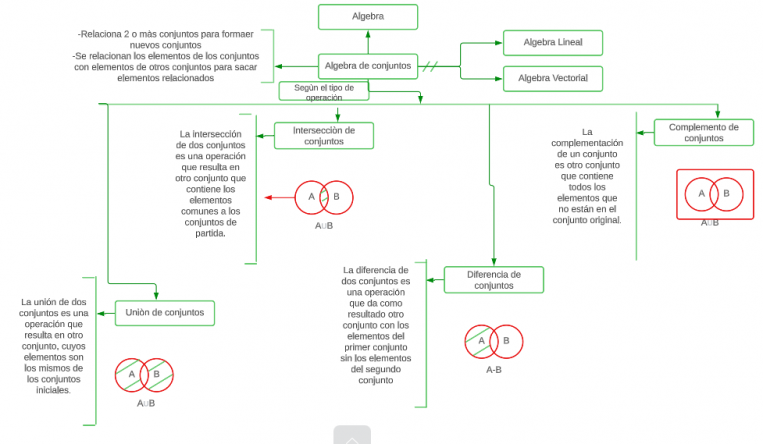
[[Archivo:Mentefacto álgebra de conjuntos.png|miniaturadeimagen|Mentefacto Conceptual Álgebra de Conjuntos|763x763px|centro]] | |||
[[Archivo:Mentefacto álgebra de conjuntos.png | ----'''<big>Paquete Proposicional:</big>''' | ||
'''Supraordinada''' | |||
P1. Toda Álgebra de Conjuntos es Álgebra. | |||
'''Isoordinadas''' | |||
P2.1 Toda Álgebra de Conjuntos es la relación de 2 o más conjuntos para formar nuevos conjuntos. | P2.1 Toda Álgebra de Conjuntos es la relación de 2 o más conjuntos para formar nuevos conjuntos. | ||
P2.2 Toda Álgebra de Conjuntos relaciona los elementos de diferentes conjuntos con diferentes elementos para sacar elementos relacionados. | P2.2 Toda Álgebra de Conjuntos relaciona los elementos de diferentes conjuntos con diferentes elementos para sacar elementos relacionados. | ||
'''Exclusiones''' | |||
P3.1 Ningún Álgebra de Conjuntos es Álgebra Lineal. | P3.1 Ningún Álgebra de Conjuntos es Álgebra Lineal. | ||
P3.2 Ningún Álgebra de Conjuntos es Álgebra Vectorial. | P3.2 Ningún Álgebra de Conjuntos es Álgebra Vectorial. | ||
'''Infraordinadas:''' | |||
P4.1 Algún Álgebra de Conjuntos es Unión de Conjuntos. | P4.1 Algún Álgebra de Conjuntos es Unión de Conjuntos. | ||
| Línea 40: | Línea 27: | ||
P4.4 Algún Álgebra de Conjuntos es Complementación de conjuntos. | P4.4 Algún Álgebra de Conjuntos es Complementación de conjuntos. | ||
----<gallery caption="Mentefactos Proposicionales"> | |||
Archivo:Ia.png|P1. Toda Álgebra de Conjuntos es Álgebra. | |||
Archivo:Aa.png|P2.1 Toda Álgebra de Conjuntos es la relación de 2 o más conjuntos para formar nuevos conjuntos. | |||
Archivo:Aa.png|P2.2 Toda Álgebra de Conjuntos relaciona los elementos de diferentes conjuntos con diferentes elementos para sacar elementos relacionados. | |||
Archivo:E.png|P3.1 Ningún Álgebra de Conjuntos es Álgebra Lineal. | |||
Archivo:E.png|P3.2 Ningún Álgebra de Conjuntos es Álgebra Vectorial. | |||
Archivo:Ai.png|P4.1 Algún Álgebra de Conjuntos es Unión de Conjuntos. | |||
Archivo:Ai.png|P4.2 Algún Álgebra de Conjuntos es Intersección de Conjuntos. | |||
Archivo:Ai.png|P4.3 Algún Álgebra de Conjuntos es Diferencia de Conjuntos. | |||
Archivo:Ai.png|P4.4 Algún Álgebra de Conjuntos es Complementación de conjuntos. | |||
</gallery> | |||
----'''<big>Argumentaciones:</big>''' | |||
'''P1. Toda Álgebra de Conjuntos es Álgebra.''' | |||
Porque los conjuntos tienen nombre y usualmente se los representan con letras mayúsculas y también porque sus operaciones básicas representan operadores algebraicos. Ejm: A U B | Porque los conjuntos tienen nombre y usualmente se los representan con letras mayúsculas y también porque sus operaciones básicas representan operadores algebraicos. Ejm: A U B | ||
'''P2.1 Toda Álgebra de Conjuntos es la relación de 2 o más conjuntos para formar nuevos conjuntos.''' | |||
La función del álgebra de conjuntos es tomar varios conjuntos y realizar algunas operaciones respectivas para acabar con un solo conjunto de elementos que se pueda representar como un nuevo conjunto. | |||
'''P2.2 Toda Álgebra de Conjuntos relaciona los elementos de diferentes conjuntos con diferentes elementos para sacar elementos relacionados'''. | |||
Los elementos relacionados pueden ser repetidos o no repetidos, pero la comparación que se hace entre conjuntos puede delimitarlos y sacar uno o más conjuntos nuevos que tengan elementos de los otros conjuntos. | |||
El álgebra vectorial se usa especialmente para representar magnitudes, posiciones, etc. y es una manera más fácil de resolver problemas de la vida cotidiana y problemas de física especialmente. Mientras que el álgebra de conjuntos se enfoca en analizar las relaciones entre conjuntos de elementos. | |||
'''P3.1 Ningún Álgebra de Conjuntos es Álgebra Lineal.''' | |||
El álgebra lineal también usa letras para representar valores no conocidos, pero los utiliza en ecuaciones lineales, inecuaciones lineales, matrices, determinantes, etc. Mientras que el álgebra de conjuntos se enfoca en analizar las relaciones entre conjuntos de elementos. | |||
'''P3.2 Ningún Álgebra de Conjuntos es Álgebra Vectorial.''' | |||
El álgebra vectorial se usa especialmente para representar magnitudes, posiciones, etc. y es una manera más fácil de resolver problemas de la vida cotidiana y problemas de física, especialmente. Mientras que el álgebra de conjuntos se enfoca en analizar las relaciones entre conjuntos de elementos. | |||
'''P4.1 Algún Álgebra de Conjuntos es Unión de Conjuntos'''. | |||
La unión de dos conjuntos es una operación algebraica que resulta en otro conjunto, cuyos elementos son los mismos de los conjuntos iniciales. | La unión de dos conjuntos es una operación algebraica que resulta en otro conjunto, cuyos elementos son los mismos de los conjuntos iniciales. | ||
'''P4.2 Algún Álgebra de Conjuntos es Intersección de Conjuntos.''' | |||
La intersección de dos conjuntos es una operación algebraica que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. | La intersección de dos conjuntos es una operación algebraica que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida. | ||
'''P4.3 Algún Álgebra de Conjuntos es Diferencia de Conjuntos.''' | |||
La diferencia de dos conjuntos es una operación algebraica que da como resultado otro conjunto con los elementos del primer conjunto sin los elementos del segundo conjunto. | La diferencia de dos conjuntos es una operación algebraica que da como resultado otro conjunto con los elementos del primer conjunto sin los elementos del segundo conjunto. | ||
'''P4.4 Algún Álgebra de Conjuntos es Complementación de conjuntos.''' | |||
La complementación de un conjunto es otro conjunto que contiene todos los elementos que no están en el conjunto original, o en otras palabras es la diferencia entre el “Conjunto Universo” y el “Conjunto dado”. | La complementación de un conjunto es otro conjunto que contiene todos los elementos que no están en el conjunto original, o en otras palabras es la diferencia entre el “Conjunto Universo” y el “Conjunto dado”. | ||
----<big>'''Referencias:'''</big> | |||
Castillo, C. I. (n.d.). Teoría de Conjuntos . <nowiki>https://www.uv.es/ivorra/Libros/TC.pdf</nowiki> | Castillo, C. I. (n.d.). Teoría de Conjuntos . <nowiki>https://www.uv.es/ivorra/Libros/TC.pdf</nowiki> | ||
Revisión actual - 00:35 1 ago 2023
Paquete Proposicional:
Supraordinada
P1. Toda Álgebra de Conjuntos es Álgebra.
Isoordinadas
P2.1 Toda Álgebra de Conjuntos es la relación de 2 o más conjuntos para formar nuevos conjuntos.
P2.2 Toda Álgebra de Conjuntos relaciona los elementos de diferentes conjuntos con diferentes elementos para sacar elementos relacionados.
Exclusiones
P3.1 Ningún Álgebra de Conjuntos es Álgebra Lineal.
P3.2 Ningún Álgebra de Conjuntos es Álgebra Vectorial.
Infraordinadas:
P4.1 Algún Álgebra de Conjuntos es Unión de Conjuntos.
P4.2 Algún Álgebra de Conjuntos es Intersección de Conjuntos.
P4.3 Algún Álgebra de Conjuntos es Diferencia de Conjuntos.
P4.4 Algún Álgebra de Conjuntos es Complementación de conjuntos.
- Mentefactos Proposicionales
P1. Toda Álgebra de Conjuntos es Álgebra.
P2.1 Toda Álgebra de Conjuntos es la relación de 2 o más conjuntos para formar nuevos conjuntos.
P2.2 Toda Álgebra de Conjuntos relaciona los elementos de diferentes conjuntos con diferentes elementos para sacar elementos relacionados.
P3.1 Ningún Álgebra de Conjuntos es Álgebra Lineal.
P3.2 Ningún Álgebra de Conjuntos es Álgebra Vectorial.
P4.1 Algún Álgebra de Conjuntos es Unión de Conjuntos.
P4.2 Algún Álgebra de Conjuntos es Intersección de Conjuntos.
P4.3 Algún Álgebra de Conjuntos es Diferencia de Conjuntos.
P4.4 Algún Álgebra de Conjuntos es Complementación de conjuntos.
Argumentaciones:
P1. Toda Álgebra de Conjuntos es Álgebra.
Porque los conjuntos tienen nombre y usualmente se los representan con letras mayúsculas y también porque sus operaciones básicas representan operadores algebraicos. Ejm: A U B
P2.1 Toda Álgebra de Conjuntos es la relación de 2 o más conjuntos para formar nuevos conjuntos.
La función del álgebra de conjuntos es tomar varios conjuntos y realizar algunas operaciones respectivas para acabar con un solo conjunto de elementos que se pueda representar como un nuevo conjunto.
P2.2 Toda Álgebra de Conjuntos relaciona los elementos de diferentes conjuntos con diferentes elementos para sacar elementos relacionados.
Los elementos relacionados pueden ser repetidos o no repetidos, pero la comparación que se hace entre conjuntos puede delimitarlos y sacar uno o más conjuntos nuevos que tengan elementos de los otros conjuntos.
P3.1 Ningún Álgebra de Conjuntos es Álgebra Lineal.
El álgebra lineal también usa letras para representar valores no conocidos, pero los utiliza en ecuaciones lineales, inecuaciones lineales, matrices, determinantes, etc. Mientras que el álgebra de conjuntos se enfoca en analizar las relaciones entre conjuntos de elementos.
P3.2 Ningún Álgebra de Conjuntos es Álgebra Vectorial.
El álgebra vectorial se usa especialmente para representar magnitudes, posiciones, etc. y es una manera más fácil de resolver problemas de la vida cotidiana y problemas de física, especialmente. Mientras que el álgebra de conjuntos se enfoca en analizar las relaciones entre conjuntos de elementos.
P4.1 Algún Álgebra de Conjuntos es Unión de Conjuntos.
La unión de dos conjuntos es una operación algebraica que resulta en otro conjunto, cuyos elementos son los mismos de los conjuntos iniciales.
P4.2 Algún Álgebra de Conjuntos es Intersección de Conjuntos.
La intersección de dos conjuntos es una operación algebraica que resulta en otro conjunto que contiene los elementos comunes a los conjuntos de partida.
P4.3 Algún Álgebra de Conjuntos es Diferencia de Conjuntos.
La diferencia de dos conjuntos es una operación algebraica que da como resultado otro conjunto con los elementos del primer conjunto sin los elementos del segundo conjunto.
P4.4 Algún Álgebra de Conjuntos es Complementación de conjuntos.
La complementación de un conjunto es otro conjunto que contiene todos los elementos que no están en el conjunto original, o en otras palabras es la diferencia entre el “Conjunto Universo” y el “Conjunto dado”.
Referencias:
Castillo, C. I. (n.d.). Teoría de Conjuntos . https://www.uv.es/ivorra/Libros/TC.pdf