Diferencia entre revisiones de «Mentefacto conceptual multiplicacion»

Revisión actual - 16:42 3 ago 2023

Paquete proposicional

Supraordinada

P1: Toda multiplicación es operación aritmética.

Isoordinadas

P.2.1: Toda multiplicación representa una suma sucesiva de sumandos iguales.

P.2.2: Toda multiplicación tiene términos denominados factores y producto.

P.2.3: Toda multiplicación utiliza el operador aspa, representado con el símbolo “x”

Exclusiones

P.3.1 : Ninguna multiplicación es suma.

P.3.2 : Ninguna multiplicación es división.

P.3.3: Ninguna multiplicación es resta.

Mentefactos Proposicionales
P1: Toda multiplicación es operación aritmética.
P.2.1: Toda multiplicación representa una suma sucesiva de sumandos iguales.
P.2.2: Toda multiplicación tiene términos denominados factores y producto.
P.2.3: Toda multiplicación utiliza el operador aspa, representado con el símbolo “x”
P.3.1 : Ninguna multiplicación es suma.
P.3.2 : Ninguna multiplicación es división.
P.3.3: Ninguna multiplicación es resta.

Argumentaciones

P1: Toda multiplicación es operación aritmética.

La multiplicación es una operación aritmética, porque en esta intervienen cantidades y operadores para la obtención de un resultado al sumar varias veces el mismo número.

P.2.1: Toda multiplicación representa una suma sucesiva de sumandos iguales.

Uno de los factores de la multiplicación se suma por sí mismo las veces que indique él otro factor.

P.2.2: Toda multiplicación tiene términos denominados factores y producto.

Porque la multiplicación al ser una operación aritmética debe tener términos que la compongan. Los términos a multiplicar se denominan factores y el resultado de esta operación se denomina producto.

P.2.3: Toda multiplicación utiliza el operador aspa, representado con el símbolo “x”

Porque cada operación aritmética es representada por un operador distinto, en el caso de la multiplicación es “x”, llamado aspa.

P.3.1: Ninguna multiplicación es suma.

Porque la multiplicación es la suma consecutiva del mismo sumando (determinado por cualquier de los factores) la cantidad de veces dictada por el otro factor, mientras que, la suma es el añadir o unir una cantidad a otra, estas cantidades llamadas sumandos no necesariamente deben ser iguales.

P.3.2 : Ninguna multiplicación es división.

Porque la multiplicación es la suma consecutiva del mismo sumando (determinado por cualquier de los factores) una cantidad de veces determinada por el otro factor, mientras que, la división descompone un número, en tantas partes como así lo indique el otro número.

P.3.3: Ninguna multiplicación es resta.

Porque la multiplicación es la suma consecutiva del mismo sumando (determinado por cualquier de los factores) una cantidad de veces determinada por el otro factor, mientras que, la resta es un tipo de suma que utiliza cantidades negativas.

@@ Línea 1: / Línea 1: @@
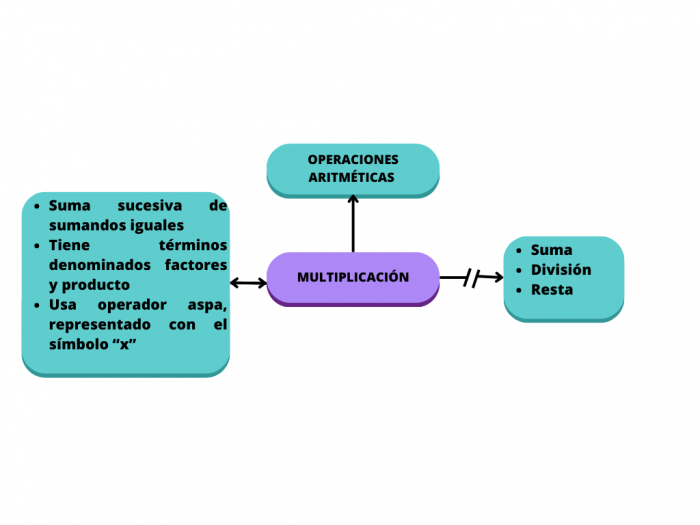
-[[Archivo:Mentefacto conceptual la multiplicacion .png|centro|miniaturadeimagen|558x558px|Mentefacto conceptual]]
+[[Archivo:Mentefacto Multiplicación.png|centro|miniaturadeimagen|700x700px]]
+----'''<big>Paquete proposicional</big>'''
-=== '''<big>Paquete proposicional</big>''' ===
+'''Supraordinada'''
-'''Supraordinarias'''
-P1: Toda multiplicación es operación aritmética .
+P1: Toda multiplicación es operación aritmética.
 ==== Isoordinadas ====
-P2: Toda multiplicación es una suma abreviada de sumandos iguales.
+P.2.1: Toda multiplicación representa una suma sucesiva de sumandos iguales.
-P.2.1: Toda multiplicación es operación con operadores (x).
+P.2.2: Toda multiplicación tiene términos denominados factores y producto.
-P2.2: Toda multiplicación es operación con los términos factores y producto .
+P.2.3: Toda multiplicación utiliza el operador aspa, representado con el símbolo “x”
 ==== Exclusiones ====
-P3 : Ninguna multiplicación es adición .
+P.3.1 : Ninguna multiplicación es suma.
-P3.1 : Ninguna multiplicación es sustracción .
+P.3.2 : Ninguna multiplicación es división.
-P3.2: Ninguna multiplicación es división .
+P.3.3: Ninguna multiplicación es resta.
+----<gallery caption="Mentefactos Proposicionales">
+Archivo:Ia.png|P1: Toda multiplicación es operación aritmética.
+Archivo:Capturaas.png|P.2.1: Toda multiplicación representa una suma sucesiva de sumandos iguales.
+Archivo:Cptas.png|P.2.2: Toda multiplicación tiene términos denominados factores y producto.
+Archivo:Ejepas.png|P.2.3: Toda multiplicación utiliza el operador aspa, representado con el símbolo “x”
+Archivo:E.png|P.3.1 : Ninguna multiplicación es suma.
+Archivo:E.png|P.3.2 : Ninguna multiplicación es división.
+Archivo:E.png|P.3.3: Ninguna multiplicación es resta.
+</gallery>
+----'''<big>Argumentaciones</big>'''
-==== Infraordinadas ====
+'''P1: Toda multiplicación es operación aritmética.'''
-'''<big>Mentefactos proposicionales</big>'''
-P1: Toda multiplicación es operación aritmética .
+La multiplicación es una operación aritmética, porque en esta intervienen cantidades y operadores para la obtención de un resultado al sumar varias veces el mismo número.
-[[Archivo:Captura de pantalla 20230110 094016.png|centro|miniaturadeimagen|195x195px|p1]]
+'''P.2.1: Toda multiplicación representa una suma sucesiva de sumandos iguales.'''
-P2: Toda multiplicación es una suma abreviada de sumandos iguales.
+Uno de los factores de la multiplicación se suma por sí mismo las veces que indique él otro factor.
-[[Archivo:Captura de pantalla 20230110 094137.png|centro|miniaturadeimagen|195x195px|p2]]
+'''P.2.2: Toda multiplicación tiene términos denominados factores y producto.'''
-P.2.1: Toda multiplicación es operación con operadores (x).
+Porque la multiplicación al ser una operación aritmética debe tener términos que la compongan. Los términos a multiplicar se denominan factores y el resultado de esta operación se denomina producto.
-[[Archivo:Captura de pantalla 20230110 094137.png|centro|miniaturadeimagen|195x195px|p2.1]]
+'''P.2.3: Toda multiplicación utiliza el operador aspa, representado con el símbolo “x”'''
-P2.2: Toda multiplicación es operación con los términos factores y producto .
+Porque cada operación aritmética es representada por un operador distinto, en el caso de la multiplicación es “x”, llamado aspa.
-[[Archivo:Captura de pantalla 20230110 094137.png|centro|miniaturadeimagen|195x195px|p2.2]]
+'''P.3.1:  Ninguna multiplicación es suma.'''
-P3 : Ninguna multiplicación es adición .
+Porque la multiplicación es la suma consecutiva del mismo sumando (determinado por cualquier de los factores) la cantidad de veces dictada por el otro factor, mientras que, la suma es el añadir o unir una cantidad a otra, estas cantidades llamadas sumandos no necesariamente deben ser iguales.
-[[Archivo:Captura de pantalla 20230110 094125.png|centro|miniaturadeimagen|195x195px|p3]]
+'''P.3.2 : Ninguna multiplicación es división.'''
-P3.1 : Ninguna multiplicación es sustracción .
+Porque la multiplicación es la suma consecutiva del mismo sumando (determinado por cualquier de los factores) una cantidad de veces determinada por el otro factor, mientras que, la división descompone un número, en tantas partes como así lo indique el otro número.
-[[Archivo:Captura de pantalla 20230110 094125.png|centro|miniaturadeimagen|195x195px|p3.1]]
+'''P.3.3: Ninguna multiplicación es resta.'''
-P3.2: Ninguna multiplicación es división .
+Porque la multiplicación es la suma consecutiva del mismo sumando (determinado por cualquier de los factores) una cantidad de veces determinada por el otro factor, mientras que, la resta es un tipo de suma que utiliza cantidades negativas.
-[[Archivo:Captura de pantalla 20230110 094125.png|centro|miniaturadeimagen|195x195px|p3.2]]
-'''<big>Argumentaciones</big>'''
-'''P1: Toda multiplicación es operación aritmética .'''
-La multiplicación es una operación matemática fundamental que se utiliza para encontrar el resultado de la combinación de dos o más números. La multiplicación implica la adición repetida de un número en sí mismo, y esta operación siempre se puede expresar en términos de la aritmética básica.
-'''P2: Toda multiplicación es una suma abreviada de sumandos iguales .'''
-La multiplicación es una operación matemática que consiste en sumar un número consigo mismo un número determinado de veces. Por ejemplo, 3 x 4 es lo mismo que sumar 3 cuatro veces: 3 + 3 + 3 + 3 = 12. En este caso, 3 es el sumando y 4 es el número de veces que se debe sumar el sumando. Por lo tanto, la multiplicación es una suma abreviada de sumandos iguales.
-'''P.2.1: Toda multiplicación es operaciP1: Toda multiplicación es operación aritmética con operadores (x).'''
-La multiplicación se representa por el operador "x", que indica la operación de multiplicar dos o más números. Por ejemplo, 2 x 3 = 6, donde 2 y 3 son los factores y 6 es el producto. La multiplicación es una operación fundamental en matemáticas y se utiliza ampliamente en cálculos y resolución de problemas.
-'''P2.2: Toda multiplicación es operación con los términos factores y producto .'''
-La multiplicación es una operación binaria que involucra dos o más números, llamados factores. La multiplicación se representa con el operador "x" o el punto ".", y el resultado de la multiplicación se llama producto.
-'''P3 : Ninguna multiplicación es adición .'''
-La multiplicación y la adición son dos operaciones matemáticas diferentes. La adición implica la combinación de dos o más números para obtener un total, mientras que la multiplicación implica la repetición de un número un determinado número de veces. Por lo tanto, la multiplicación no puede ser igual a la adición.
-'''P3.1 : Ninguna multiplicación es sustracción .'''
-La sustracción es una operación matemática que implica la eliminación de un número de otro para obtener la diferencia. La multiplicación, por otro lado, es una operación matemática que implica la combinación de dos o más números para obtener un producto. Por lo tanto, la multiplicación no puede ser igual a la sustracción.
-'''P3.2: Ninguna multiplicación es división .'''
-La división es una operación matemática que implica la separación de un número en partes iguales. La multiplicación, por otro lado, implica la combinación de dos o más números para obtener un producto. Aunque la multiplicación y la división están relacionadas, ya que una es la operación inversa de la otra, son dos operaciones diferentes. Por lo tanto, la multiplicación no puede ser igual a la división.

Diferencia entre revisiones de «Mentefacto conceptual multiplicacion»

Revisión actual - 16:42 3 ago 2023

Isoordinadas

Exclusiones

Menú de navegación

Buscar