Diferencia entre revisiones de «Mentefacto Conceptual Número Fraccionario»
(Implementar ejemplos) |
Sin resumen de edición |
||
| (No se muestra una edición intermedia de otro usuario) | |||
| Línea 1: | Línea 1: | ||
[[Archivo:Mentefacto Numero Fraccionario.png|centro|marco|Mentefacto conceptual de número fraccionario]] | [[Archivo:Mentefacto Numero Fraccionario.png|centro|marco|Mentefacto conceptual de número fraccionario]]'''<big>Paquete Proposicional</big>''' | ||
'''Supraordinada''' | |||
P1. Todo número fraccionario es número racional. | P1. Todo número fraccionario es número racional. | ||
'''Isoordinadas''' | |||
P2.1. Todo número fraccionario representa un cociente no efectuado de números. | P2.1. Todo número fraccionario representa un cociente no efectuado de números. | ||
P2.2. Todo número fraccionario tiene estructura: numerador 0 y denominador 0 y 1. | P2.2. Todo número fraccionario tiene estructura: numerador 0 y denominador 0 y 1. | ||
'''Exclusión''' | |||
P3. Ningún número fraccionario es número entero. | P3. Ningún número fraccionario es número entero. | ||
'''Infraordinadas''' | |||
P4.1. Algún número fraccionario según el valor de sus partes es fracción propia. | P4.1. Algún número fraccionario según el valor de sus partes es fracción propia. | ||
| Línea 20: | Línea 22: | ||
P4.2.1. Algún número fraccionario según el valor de sus partes es fracción aparente. | P4.2.1. Algún número fraccionario según el valor de sus partes es fracción aparente. | ||
----<gallery caption="Mentefactos Proposicionales"> | |||
Archivo:Ai.png|P1. Todo número fraccionario es número racional. | |||
Archivo:Aa.png|P2.1. Todo número fraccionario representa un cociente no efectuado de números. | |||
Archivo:Aa.png|P2.2. Todo número fraccionario tiene estructura: numerador ≠ 0 y denominador ≠ 0 y 1. | |||
Archivo:E.png|P3. Ningún número fraccionario es número entero. | |||
Archivo:E.png|P4.1. Algún número fraccionario según el valor de sus partes es fracción propia. | |||
Archivo:Ai.png|P4.2. Algún número fraccionario según el valor de sus partes es fracción impropia. | |||
Archivo:Ai.png|P4.2.1. Algún número fraccionario según el valor de sus partes es fracción aparente. | |||
</gallery> | |||
----'''Argumentaciones''' | |||
'''P1. Todo número fraccionario es número racional.''' | |||
Porque un número racional es aquel que puede ser expresado de diferentes formas, en este caso como una fracción, donde tanto el numerador como el denominador tendrán un valor numérico. Esto hace que cualquier número fraccionario pueda expresarse como un número racional. | Porque un número racional es aquel que puede ser expresado de diferentes formas, en este caso como una fracción, donde tanto el numerador como el denominador tendrán un valor numérico. Esto hace que cualquier número fraccionario pueda expresarse como un número racional. | ||
''Ejemplo:'' <math>1/2</math> | ''Ejemplo:'' <math>1/2</math> | ||
'''P2.1. Todo número fraccionario representa un cociente no efectuado de números.''' | |||
Porque un número fraccionario representa la cantidad de partes iguales en las que se divide un objeto o una cantidad. Estos números expresan una división entre el numerador (el número de partes que se toman) y el denominador (el número total de partes en que se divide el objeto o la cantidad). | Porque un número fraccionario representa la cantidad de partes iguales en las que se divide un objeto o una cantidad. Estos números expresan una división entre el numerador (el número de partes que se toman) y el denominador (el número total de partes en que se divide el objeto o la cantidad). | ||
''Ejemplo:'' <math>1/4=1\div4</math> | ''Ejemplo:'' <math>1/4=1\div4</math> | ||
'''P2.2. Todo número fraccionario tiene estructura: numerador ≠ 0 y denominador ≠ 0 y 1.''' | |||
Porque el numerador es el número de partes que se toma de un todo, mientras que el denominador representa el número total de partes en que se divide ese todo. Es importante que el numerador no sea 0 para que no se vuelva un número entero, asimismo el denominador no puede ser 0 ni 1 porque en el primer caso se forma un número irracional y en el segundo un número entero. | Porque el numerador es el número de partes que se toma de un todo, mientras que el denominador representa el número total de partes en que se divide ese todo. Es importante que el numerador no sea 0 para que no se vuelva un número entero, asimismo el denominador no puede ser 0 ni 1 porque en el primer caso se forma un número irracional y en el segundo un número entero. | ||
''Ejemplo:'' <math>5/2</math> | ''Ejemplo:'' <math>5/2</math> | ||
'''P3. Ningún número fraccionario es número entero.''' | |||
Porque un número entero es aquel que no tiene decimales, es decir, que se expresa sin una fracción ni puntos decimales; mientras que un número fraccionario es aquel que se expresa como una fracción, es decir, como una división de dos números. | Porque un número entero es aquel que no tiene decimales, es decir, que se expresa sin una fracción ni puntos decimales; mientras que un número fraccionario es aquel que se expresa como una fracción, es decir, como una división de dos números. | ||
''Ejemplo:'' <math>2/3\neq5</math> | ''Ejemplo:'' <math>2/3\neq5</math> | ||
'''P4.1. Algún número fraccionario según el valor de sus partes es fracción propia.''' | |||
Porque una fracción propia es aquella cuyo numerador es menor que su denominador; es decir que al momento de transformarle a un número decimal, el resultado del mismo nos dará un número cuya cantidad es menor a 1. | Porque una fracción propia es aquella cuyo numerador es menor que su denominador; es decir que al momento de transformarle a un número decimal, el resultado del mismo nos dará un número cuya cantidad es menor a 1. | ||
''Ejemplo:'' <math>4/7<1</math> | ''Ejemplo:'' <math>4/7<1</math> | ||
'''P4.2. Algún número fraccionario según el valor de sus partes es fracción impropia.''' | |||
Porque una fracción impropia es aquella cuyo numerador es mayor a su denominador; es decir que al momento de transformarle a un número decimal, el resultado del mismo nos dará un número cuya cantidad es mayor a 1. | Porque una fracción impropia es aquella cuyo numerador es mayor a su denominador; es decir que al momento de transformarle a un número decimal, el resultado del mismo nos dará un número cuya cantidad es mayor a 1. | ||
''Ejemplo:'' <math>9/2>1</math> | ''Ejemplo:'' <math>9/2>1</math> | ||
'''P4.2.1. Algún número fraccionario según el valor de sus partes es fracción aparente.''' | |||
Porque una fracción aparente es aquella cuyo numerador es igual a su denominador; es decir que al momento de simplificarlos, el resultado del mismo nos dará un número cuya cantidad será igual a la unidad. | Porque una fracción aparente es aquella cuyo numerador es igual a su denominador; es decir que al momento de simplificarlos, el resultado del mismo nos dará un número cuya cantidad será igual a la unidad. | ||
''Ejemplo:'' <math>3/3=1</math> | ''Ejemplo:'' <math>3/3=1</math> | ||
----'''<big>Referencias</big>''' | |||
*Chavarro , M. (n.d.). TOMi.digital - Números Fraccionarios. TOMi.digital. Retrieved April 21, 2023, from https://tomi.digital/es/47551/numeros-fraccionarios?utm_source=google&utm_medium=seo | |||
* Chavarro , M. (n.d.). TOMi.digital - Números Fraccionarios. TOMi.digital. Retrieved April 21, 2023, from https://tomi.digital/es/47551/numeros-fraccionarios?utm_source=google&utm_medium=seo | |||
* enunciados, I. D. A. B. de educación infantil con especialización en C. del medio desde las ciencias y las matemáticas F. parte del equipo de desarrollo de contenidos de S. y se encarga de la elaboración y secuenciación de. (2014, November 24). Clasificación de fracciones: propias, impropias y unitarias. Smartick. https://www.smartick.es/blog/matematicas/fracciones/clasificacion-de-fracciones/ | *enunciados, I. D. A. B. de educación infantil con especialización en C. del medio desde las ciencias y las matemáticas F. parte del equipo de desarrollo de contenidos de S. y se encarga de la elaboración y secuenciación de. (2014, November 24). Clasificación de fracciones: propias, impropias y unitarias. Smartick. https://www.smartick.es/blog/matematicas/fracciones/clasificacion-de-fracciones/ | ||
* Fracciones Propias e Impropias. (n.d.). Content.nroc.org. Retrieved April 21, 2023, from https://content.nroc.org/DevelopmentalMath.HTML5/U02L1T2/TopicText/es/textbook.html | *Fracciones Propias e Impropias. (n.d.). Content.nroc.org. Retrieved April 21, 2023, from https://content.nroc.org/DevelopmentalMath.HTML5/U02L1T2/TopicText/es/textbook.html | ||
* Gómez, M. (2008). FRACCIONES. Recursostic.educacion.es. http://recursostic.educacion.es/descartes/web/materiales_didacticos/fracciones_migv/irreducible.htm#:~:text=Las%20fracciones%20est%C3%A1n%20formadas%20por | *Gómez, M. (2008). FRACCIONES. Recursostic.educacion.es. http://recursostic.educacion.es/descartes/web/materiales_didacticos/fracciones_migv/irreducible.htm#:~:text=Las%20fracciones%20est%C3%A1n%20formadas%20por | ||
* Para que sirven las fracciones. (2020, November 7). Profesor de Mate. https://profesordemate.win/para-que-sirven-las-fracciones/ | *Para que sirven las fracciones. (2020, November 7). Profesor de Mate. https://profesordemate.win/para-que-sirven-las-fracciones/ | ||
* Smartick.Malagueño, D. G. de V. de, Málaga, es ingeniero industrial por la U. de, hijas, tiene un M. por I. y es emprendedor E. E. el responsable de desarrollo de producto y de que encajen todas las piezas del puzle de S. S. tiempo libre se lo dedica a sus dos, estudiar, & Flamenco, H. D. Y. E. (2012, August 20). Introducción a las fracciones. Smartick. https://www.smartick.es/blog/matematicas/fracciones/introduccion-a-las-fracciones/#Tipos_de_fracciones | *Smartick.Malagueño, D. G. de V. de, Málaga, es ingeniero industrial por la U. de, hijas, tiene un M. por I. y es emprendedor E. E. el responsable de desarrollo de producto y de que encajen todas las piezas del puzle de S. S. tiempo libre se lo dedica a sus dos, estudiar, & Flamenco, H. D. Y. E. (2012, August 20). Introducción a las fracciones. Smartick. https://www.smartick.es/blog/matematicas/fracciones/introduccion-a-las-fracciones/#Tipos_de_fracciones | ||
__FORZAR_TDC__ | __FORZAR_TDC__ | ||
Revisión actual - 17:35 27 jul 2023
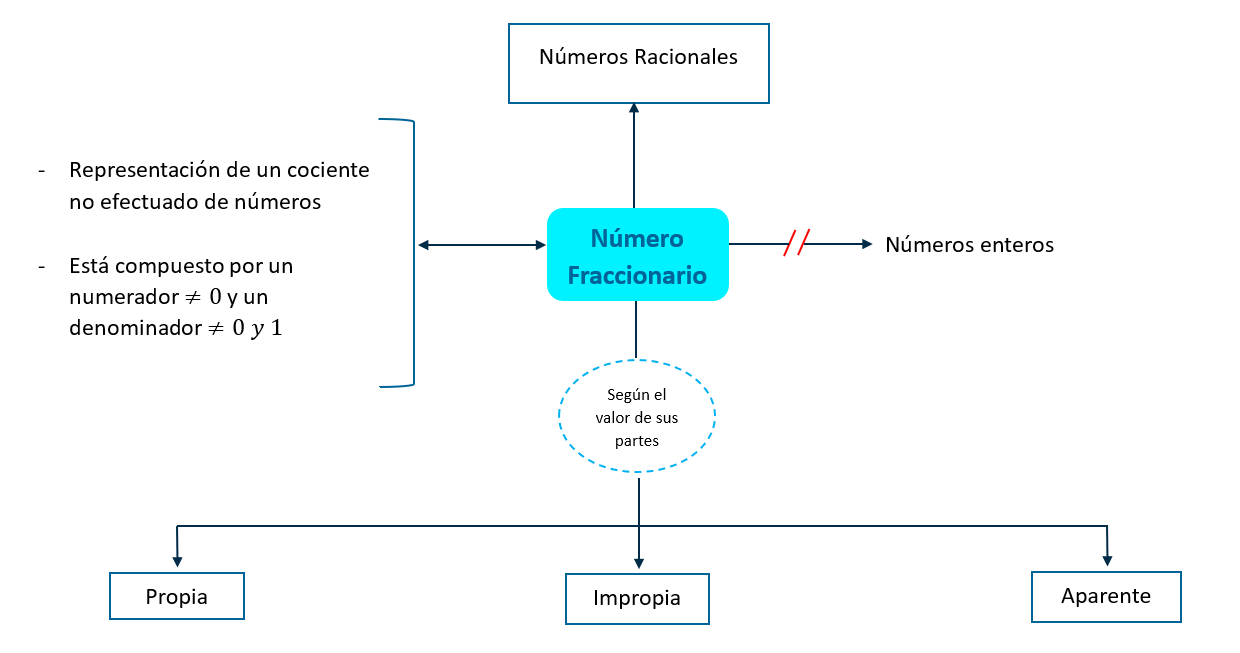
Paquete Proposicional
Supraordinada
P1. Todo número fraccionario es número racional.
Isoordinadas
P2.1. Todo número fraccionario representa un cociente no efectuado de números.
P2.2. Todo número fraccionario tiene estructura: numerador 0 y denominador 0 y 1.
Exclusión
P3. Ningún número fraccionario es número entero.
Infraordinadas
P4.1. Algún número fraccionario según el valor de sus partes es fracción propia.
P4.2. Algún número fraccionario según el valor de sus partes es fracción impropia.
P4.2.1. Algún número fraccionario según el valor de sus partes es fracción aparente.
- Mentefactos Proposicionales
P1. Todo número fraccionario es número racional.
P2.1. Todo número fraccionario representa un cociente no efectuado de números.
P2.2. Todo número fraccionario tiene estructura: numerador ≠ 0 y denominador ≠ 0 y 1.
P3. Ningún número fraccionario es número entero.
P4.1. Algún número fraccionario según el valor de sus partes es fracción propia.
P4.2. Algún número fraccionario según el valor de sus partes es fracción impropia.
P4.2.1. Algún número fraccionario según el valor de sus partes es fracción aparente.
Argumentaciones
P1. Todo número fraccionario es número racional.
Porque un número racional es aquel que puede ser expresado de diferentes formas, en este caso como una fracción, donde tanto el numerador como el denominador tendrán un valor numérico. Esto hace que cualquier número fraccionario pueda expresarse como un número racional.
Ejemplo:
P2.1. Todo número fraccionario representa un cociente no efectuado de números.
Porque un número fraccionario representa la cantidad de partes iguales en las que se divide un objeto o una cantidad. Estos números expresan una división entre el numerador (el número de partes que se toman) y el denominador (el número total de partes en que se divide el objeto o la cantidad).
Ejemplo:
P2.2. Todo número fraccionario tiene estructura: numerador ≠ 0 y denominador ≠ 0 y 1.
Porque el numerador es el número de partes que se toma de un todo, mientras que el denominador representa el número total de partes en que se divide ese todo. Es importante que el numerador no sea 0 para que no se vuelva un número entero, asimismo el denominador no puede ser 0 ni 1 porque en el primer caso se forma un número irracional y en el segundo un número entero.
Ejemplo:
P3. Ningún número fraccionario es número entero.
Porque un número entero es aquel que no tiene decimales, es decir, que se expresa sin una fracción ni puntos decimales; mientras que un número fraccionario es aquel que se expresa como una fracción, es decir, como una división de dos números.
Ejemplo:
P4.1. Algún número fraccionario según el valor de sus partes es fracción propia.
Porque una fracción propia es aquella cuyo numerador es menor que su denominador; es decir que al momento de transformarle a un número decimal, el resultado del mismo nos dará un número cuya cantidad es menor a 1.
Ejemplo:
P4.2. Algún número fraccionario según el valor de sus partes es fracción impropia.
Porque una fracción impropia es aquella cuyo numerador es mayor a su denominador; es decir que al momento de transformarle a un número decimal, el resultado del mismo nos dará un número cuya cantidad es mayor a 1.
Ejemplo:
P4.2.1. Algún número fraccionario según el valor de sus partes es fracción aparente.
Porque una fracción aparente es aquella cuyo numerador es igual a su denominador; es decir que al momento de simplificarlos, el resultado del mismo nos dará un número cuya cantidad será igual a la unidad.
Ejemplo:
Referencias
- Chavarro , M. (n.d.). TOMi.digital - Números Fraccionarios. TOMi.digital. Retrieved April 21, 2023, from https://tomi.digital/es/47551/numeros-fraccionarios?utm_source=google&utm_medium=seo
- enunciados, I. D. A. B. de educación infantil con especialización en C. del medio desde las ciencias y las matemáticas F. parte del equipo de desarrollo de contenidos de S. y se encarga de la elaboración y secuenciación de. (2014, November 24). Clasificación de fracciones: propias, impropias y unitarias. Smartick. https://www.smartick.es/blog/matematicas/fracciones/clasificacion-de-fracciones/
- Fracciones Propias e Impropias. (n.d.). Content.nroc.org. Retrieved April 21, 2023, from https://content.nroc.org/DevelopmentalMath.HTML5/U02L1T2/TopicText/es/textbook.html
- Gómez, M. (2008). FRACCIONES. Recursostic.educacion.es. http://recursostic.educacion.es/descartes/web/materiales_didacticos/fracciones_migv/irreducible.htm#:~:text=Las%20fracciones%20est%C3%A1n%20formadas%20por
- Para que sirven las fracciones. (2020, November 7). Profesor de Mate. https://profesordemate.win/para-que-sirven-las-fracciones/
- Smartick.Malagueño, D. G. de V. de, Málaga, es ingeniero industrial por la U. de, hijas, tiene un M. por I. y es emprendedor E. E. el responsable de desarrollo de producto y de que encajen todas las piezas del puzle de S. S. tiempo libre se lo dedica a sus dos, estudiar, & Flamenco, H. D. Y. E. (2012, August 20). Introducción a las fracciones. Smartick. https://www.smartick.es/blog/matematicas/fracciones/introduccion-a-las-fracciones/#Tipos_de_fracciones