Diferencia entre revisiones de «Mentefacto Cuadrilátero»
(Página creada con «centro|miniaturadeimagen|1131x1131px == Paquete proposicional: == P1: Todo cuadrilátero es polígono. P2.1: Todo cuadrilátero es una figura que tiene cuatro ángulos internos ( que suman 360°). P2.2: El cuadrilátero tiene una figura que son tetrágonos. P2.3: El cuadrilátero tiene figuras de dos dimensiones. P3.1: Ningún cuadrilátero es triángulo . P3.2: Ningún cuadrilátero es pentágono. P3.3: Ningún cuadriláte…») |
Sin resumen de edición |
||
| (No se muestran 3 ediciones intermedias de otro usuario) | |||
| Línea 1: | Línea 1: | ||
[[Archivo:Cuadrilatero (3).png|centro|miniaturadeimagen|1131x1131px]] | [[Archivo:Cuadrilatero (3).png|centro|miniaturadeimagen|1131x1131px]]'''<big>Paquete proposicional:</big>''' | ||
'''Supraordinada''' | |||
P1: Todo cuadrilátero es polígono. | P1: Todo cuadrilátero es polígono. | ||
'''Isoordinadas''' | |||
P2.1: Todo cuadrilátero es una figura que tiene cuatro ángulos internos ( que suman 360°). | P2.1: Todo cuadrilátero es una figura que tiene cuatro ángulos internos ( que suman 360°). | ||
P2.2: | P2.2: Todo cuadrilátero es tetrágono. | ||
P2.3: Todo cuadrilátero es figuras de dos dimensiones. | |||
'''Exclusiones''' | |||
P3.1: Ningún cuadrilátero es triángulo . | P3.1: Ningún cuadrilátero es triángulo. | ||
P3.2: Ningún cuadrilátero es pentágono. | P3.2: Ningún cuadrilátero es pentágono. | ||
P3.3: Ningún cuadrilátero es hexágono. | P3.3: Ningún cuadrilátero es hexágono. | ||
'''Infraordinadas''' | |||
P4.1: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros cóncavos. | P4.1: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros cóncavos. | ||
| Línea 20: | Línea 27: | ||
P4.2: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros convexos. | P4.2: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros convexos. | ||
P4.2.1: Algunos cuadriláteros convexos son paralelogramos. | P4.2.1: Algunos cuadriláteros convexos son paralelogramos. | ||
P4.2.1.1: Algunos paralelogramos son rectángulos. | P4.2.1.1: Algunos paralelogramos son rectángulos. | ||
P4.2.1.2: Algunos paralelogramos son cuadrados. | P4.2.1.2: Algunos paralelogramos son cuadrados. | ||
P4.2.1.3: Algunos paralelogramos son romboides. | P4.2.1.3: Algunos paralelogramos son romboides. | ||
P4.2.1.4: Algunos paralelogramos son rombos. | P4.2.1.4: Algunos paralelogramos son rombos. | ||
| Línea 32: | Línea 39: | ||
P4.2.2.1: Algunos cuadriláteros convexos son trapecios. | P4.2.2.1: Algunos cuadriláteros convexos son trapecios. | ||
P4.2.2.2: Algunos trapecios son trapecios escalenos. | P4.2.2.2: Algunos trapecios son trapecios escalenos. | ||
P4.2.2.3: Algunos trapecios son trapecios rectángulos. | P4.2.2.3: Algunos trapecios son trapecios rectángulos. | ||
P4.2.3.1: Algunos cuadriláteros convexos son trapezoides. | |||
P4.2.3.1: Algunos cuadriláteros convexos son trapezoides. | P4.2.3.1: Algunos cuadriláteros convexos son trapezoides. | ||
| Línea 40: | Línea 49: | ||
P4.2.3.2: Algunos trapezoides son trapezoides sistemáticos. | P4.2.3.2: Algunos trapezoides son trapezoides sistemáticos. | ||
P4.2.3.3: Algunos trapezoides son trapezoides asimétricos. | P4.2.3.3: Algunos trapezoides son trapezoides asimétricos. | ||
----<gallery caption="'''Mentefactos proposicionales'''"> | |||
Archivo:Ia.png|P1: Todo cuadrilátero es polígono. | |||
Archivo:Aa.png|P2.1: Todo cuadrilátero es una figura que tiene cuatro ángulos internos ( que suman 360°). | |||
Archivo:Aa.png|P2.2: Todo cuadrilátero es tetrágono. | |||
Archivo:E.png|P3.1: Ningún cuadrilátero es triángulo. | |||
Archivo:E.png|P3.2: Ningún cuadrilátero es pentágono. | |||
Archivo:E.png|P3.3: Ningún cuadrilátero es hexágono. | |||
Archivo:Ai.png|P4.1: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros cóncavos. | |||
Archivo:Ai.png|P4.2: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros convexos. | |||
Archivo:Ai.png|P4.2.1: Algunos cuadriláteros convexos son paralelogramos. | |||
Archivo:Ai.png|P4.2.1.1: Algunos paralelogramos son rectángulos. | |||
Archivo:Ai.png|P4.2.1.2: Algunos paralelogramos son cuadrados. | |||
Archivo:Ai.png|P4.2.1.3: Algunos paralelogramos son romboides. | |||
Archivo:Ai.png|P4.2.1.4: Algunos paralelogramos son rombos. | |||
Archivo:Ai.png|P4.2.2.1: Algunos cuadriláteros convexos son trapecios. | |||
Archivo:Ai.png|P4.2.2.2: Algunos trapecios son trapecios escalenos. | |||
Archivo:Ai.png|P4.2.2.3: Algunos trapecios son trapecios rectángulos. | |||
Archivo:Ai.png|P4.2.3.1: Algunos cuadriláteros convexos son trapezoides. | |||
Archivo:Ai.png|P4.2.3.1: Algunos cuadriláteros convexos son trapezoides. | |||
Archivo:Ai.png|P4.2.3.2: Algunos trapezoides son trapezoides sistemáticos. | |||
Archivo:Ai.png|P4.2.3.3: Algunos trapezoides son trapezoides asimétricos. | |||
</gallery> | |||
----'''<big>Análisis proposicional</big>''' | |||
'''P1: Todo cuadrilátero es polígono.''' | |||
El cuadrilátero es figura geométrica siendo un polígono que va teniendo cuatro lados, cuatro ángulos y cuatro vértices que tienen distintas formas por la geometría en el plano euclidiano. | |||
'''P2.1: El cuadrilátero tiene cuatro ángulos internos ( que suman 360°).''' | |||
El cuadrilátero debido a que puede ser dividido en dos triángulos, y la suma de los ángulos internos de un triángulo es siempre igual a 180 grados. | |||
'''P2.2: Todo cuadrilátero es tetrágono.''' | |||
El cuadrilátero tiene cuatro lados, cuatro vértices y cuatro ángulos internos, además se caracteriza por tener sus lados rectos. | |||
'''P3.1: Ningún cuadrilátero es triángulo.''' | |||
El triángulo es una figura de dos dimensiones que está formada por tres puntos no colineales, no están en una misma línea recta, que están conectados por segmentos de línea para formar tres lados y tres ángulos. | |||
'''P3.2: Ningún cuadrilátero es pentágono.''' | |||
El pentágono tiene diferentes propiedades, como pentágonos regulares con cinco lados y cinco ángulos de igual medida o los pentágonos irregulares con cinco lados y cinco ángulos de diferentes medidas. | |||
'''P3.3: Ningún cuadrilátero es hexágono.''' | |||
El hexágono es una figura geométrica con seis lados y seis vértices, que puede ser regular o irregular utilizado en diversos contextos en la naturaleza y en aplicaciones humanas. | |||
'''P4.1: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros cóncavos.''' | |||
Ya que puede tener una amplia variedad de formas y configuraciones, ya que solo necesita tener al menos un ángulo interno mayor a 180 grados para ser considerado un cuadrilátero cóncavo. | |||
'''P4.2: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros convexos.''' | |||
Ya que todos sus ángulos internos son menores a 180 grados y sus lados no se doblan hacia adentro en ninguna parte no presenta ninguna porción curvada hacia adentro en su contorno y así se consideran cuadriláteros convexos. | |||
'''P4.2.1: Algunos cuadriláteros convexos son paralelogramos.''' | |||
El paralelogramo tiene lados opuestos y congruentes, lo que significa que tienen la misma longitud y los ángulos opuestos de un paralelogramo son iguales, lo que significa que tienen la misma medida. | |||
'''P4.2.1.1: Algunos paralelogramos son rectángulos.''' | |||
Los rectángulos pueden tener diferentes tamaños y proporciones, pero siempre tendrán cuatro lados con ángulos rectos y lados opuestos de igual longitud. | |||
'''P4.2.1.2: Algunos paralelogramos son cuadrados.''' | |||
Los cuadrados se caracterizan por tener cuatro lados de igual longitud y cuatro ángulos internos de 90 grados, lo que significa que sus lados son iguales en longitud y sus ángulos son iguales en medida. | |||
'''P4.2.1.3: Algunos paralelogramos son romboides.''' | |||
Los romboides tienen los lados opuestos que son paralelos entre sí, entonces nunca se cruzan y los lados adyacentes del romboide pueden tener longitudes diferentes, lo que hace que sus ángulos internos también sean diferentes. | |||
'''P4.2.1.4: Algunos paralelogramos son rombos.''' | |||
Los rombos son polígonos más específicamente son figuras planas que se forman a partir de una cantidad finita de segmentos rectos que aparecen dispuestos de manera consecutiva en un plano. | |||
'''P4.2.2.1: Algunos cuadriláteros convexos son trapecios.''' | |||
Los trapecios solo tiene dos lados paralelos entre sí, lo que nunca se cruzarán aún así se prolonguen. Dichos lados paralelos reciben el nombre de base mayor (B) y base menor (b). | |||
'''P4.2.2.2: Algunos trapecios son trapecios escalenos.''' | |||
Los trapecios escalenos tienen sus cuatro lados desiguales, siendo sus ángulos interiores siendo diferentes entre sí y no tiene un ángulo igual ni ángulo recto. | |||
'''P4.2.2.3: Algunos trapecios son trapecios rectángulos.''' | |||
Los trapecios rectángulos tiene dos ángulos rectos, uno agudo y otro obtuso. Puede tener dos lados iguales o todos distintos, también con sus uno o dos ángulos obtusos. | |||
'''P4.2.3.1: Algunos cuadriláteros convexos son trapezoides.''' | |||
Los trapezoides es una figura geométrica plana de 4 lados de los cuales ninguno es paralelo a otro, al ser prolongados, los segmentos que forman la figura podrían cruzarse. | |||
'''P4.2.3.2: Algunos trapezoides son trapezoides sistemáticos.''' | |||
Los trapezoides sistemáticos tiene dos pares de lados consecutivos iguales, que tiene un eje de simetría, sus diagonales son perpendiculares y se cruzan en el punto medio. | |||
'''P4.2.3.3: Algunos trapezoides son trapezoides asimétricos.''' | |||
Los trapezoides asimétricos tiene su lados no paralelos, ni un eje de simetría, entonces no son paralelogramos. Pero aún así sus ángulos internos al sumarlo da 360º. | |||
----'''<big>Referencias</big>''' | |||
- Aguilar Durán, Rosa, & Inojosa, I. (2013). La geometría de los cuadriláteros en los libros de texto de educación primaria. ''Paradígma'', ''34''(2), 151–173. http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S1011-22512013000200009 | - Aguilar Durán, Rosa, & Inojosa, I. (2013). La geometría de los cuadriláteros en los libros de texto de educación primaria. ''Paradígma'', ''34''(2), 151–173. http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S1011-22512013000200009 | ||
Revisión actual - 12:52 26 jul 2023
.png)
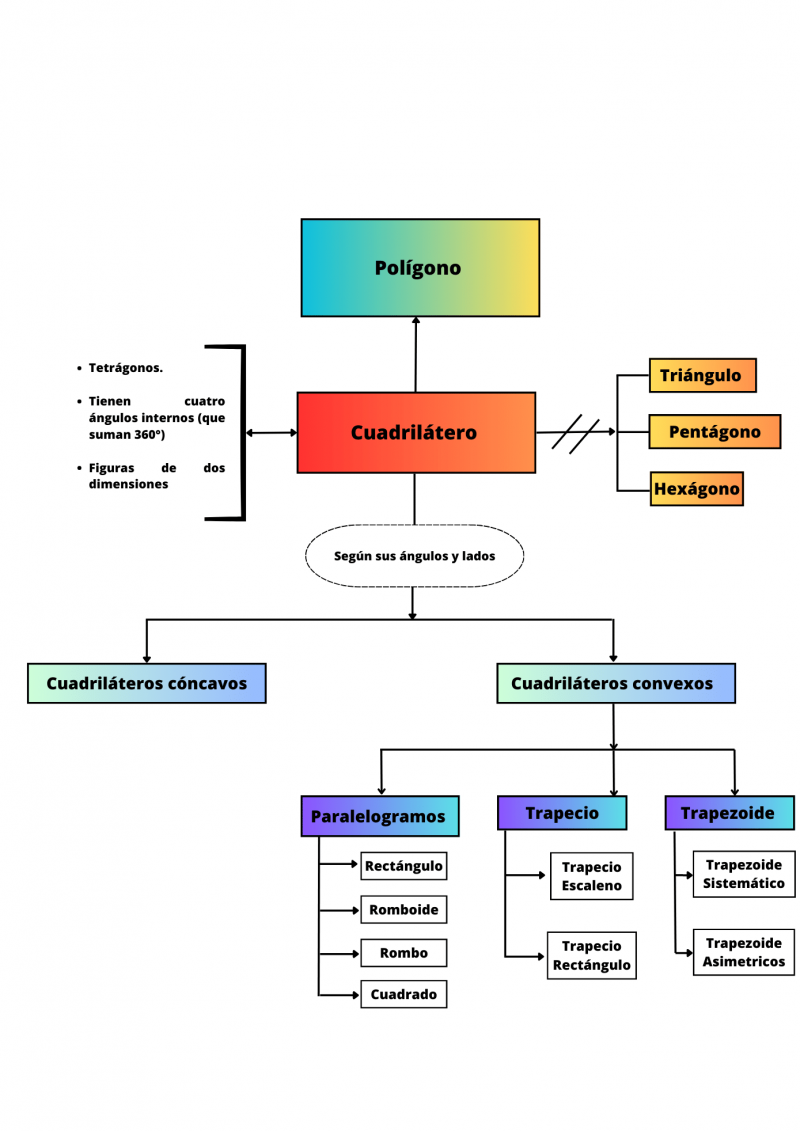
Paquete proposicional:
Supraordinada
P1: Todo cuadrilátero es polígono.
Isoordinadas
P2.1: Todo cuadrilátero es una figura que tiene cuatro ángulos internos ( que suman 360°).
P2.2: Todo cuadrilátero es tetrágono.
P2.3: Todo cuadrilátero es figuras de dos dimensiones.
Exclusiones
P3.1: Ningún cuadrilátero es triángulo.
P3.2: Ningún cuadrilátero es pentágono.
P3.3: Ningún cuadrilátero es hexágono.
Infraordinadas
P4.1: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros cóncavos.
P4.2: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros convexos.
P4.2.1: Algunos cuadriláteros convexos son paralelogramos.
P4.2.1.1: Algunos paralelogramos son rectángulos.
P4.2.1.2: Algunos paralelogramos son cuadrados.
P4.2.1.3: Algunos paralelogramos son romboides.
P4.2.1.4: Algunos paralelogramos son rombos.
P4.2.2.1: Algunos cuadriláteros convexos son trapecios.
P4.2.2.2: Algunos trapecios son trapecios escalenos.
P4.2.2.3: Algunos trapecios son trapecios rectángulos.
P4.2.3.1: Algunos cuadriláteros convexos son trapezoides.
P4.2.3.1: Algunos cuadriláteros convexos son trapezoides.
P4.2.3.2: Algunos trapezoides son trapezoides sistemáticos.
P4.2.3.3: Algunos trapezoides son trapezoides asimétricos.
- Mentefactos proposicionales
P1: Todo cuadrilátero es polígono.
P2.1: Todo cuadrilátero es una figura que tiene cuatro ángulos internos ( que suman 360°).
P2.2: Todo cuadrilátero es tetrágono.
P3.1: Ningún cuadrilátero es triángulo.
P3.2: Ningún cuadrilátero es pentágono.
P3.3: Ningún cuadrilátero es hexágono.
P4.1: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros cóncavos.
P4.2: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros convexos.
P4.2.1: Algunos cuadriláteros convexos son paralelogramos.
P4.2.1.1: Algunos paralelogramos son rectángulos.
P4.2.1.2: Algunos paralelogramos son cuadrados.
P4.2.1.3: Algunos paralelogramos son romboides.
P4.2.1.4: Algunos paralelogramos son rombos.
P4.2.2.1: Algunos cuadriláteros convexos son trapecios.
P4.2.2.2: Algunos trapecios son trapecios escalenos.
P4.2.2.3: Algunos trapecios son trapecios rectángulos.
P4.2.3.1: Algunos cuadriláteros convexos son trapezoides.
P4.2.3.1: Algunos cuadriláteros convexos son trapezoides.
P4.2.3.2: Algunos trapezoides son trapezoides sistemáticos.
P4.2.3.3: Algunos trapezoides son trapezoides asimétricos.
Análisis proposicional
P1: Todo cuadrilátero es polígono.
El cuadrilátero es figura geométrica siendo un polígono que va teniendo cuatro lados, cuatro ángulos y cuatro vértices que tienen distintas formas por la geometría en el plano euclidiano.
P2.1: El cuadrilátero tiene cuatro ángulos internos ( que suman 360°).
El cuadrilátero debido a que puede ser dividido en dos triángulos, y la suma de los ángulos internos de un triángulo es siempre igual a 180 grados.
P2.2: Todo cuadrilátero es tetrágono.
El cuadrilátero tiene cuatro lados, cuatro vértices y cuatro ángulos internos, además se caracteriza por tener sus lados rectos.
P3.1: Ningún cuadrilátero es triángulo.
El triángulo es una figura de dos dimensiones que está formada por tres puntos no colineales, no están en una misma línea recta, que están conectados por segmentos de línea para formar tres lados y tres ángulos.
P3.2: Ningún cuadrilátero es pentágono.
El pentágono tiene diferentes propiedades, como pentágonos regulares con cinco lados y cinco ángulos de igual medida o los pentágonos irregulares con cinco lados y cinco ángulos de diferentes medidas.
P3.3: Ningún cuadrilátero es hexágono.
El hexágono es una figura geométrica con seis lados y seis vértices, que puede ser regular o irregular utilizado en diversos contextos en la naturaleza y en aplicaciones humanas.
P4.1: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros cóncavos.
Ya que puede tener una amplia variedad de formas y configuraciones, ya que solo necesita tener al menos un ángulo interno mayor a 180 grados para ser considerado un cuadrilátero cóncavo.
P4.2: Algunos cuadriláteros según sus ángulos y lados son cuadriláteros convexos.
Ya que todos sus ángulos internos son menores a 180 grados y sus lados no se doblan hacia adentro en ninguna parte no presenta ninguna porción curvada hacia adentro en su contorno y así se consideran cuadriláteros convexos.
P4.2.1: Algunos cuadriláteros convexos son paralelogramos.
El paralelogramo tiene lados opuestos y congruentes, lo que significa que tienen la misma longitud y los ángulos opuestos de un paralelogramo son iguales, lo que significa que tienen la misma medida.
P4.2.1.1: Algunos paralelogramos son rectángulos.
Los rectángulos pueden tener diferentes tamaños y proporciones, pero siempre tendrán cuatro lados con ángulos rectos y lados opuestos de igual longitud.
P4.2.1.2: Algunos paralelogramos son cuadrados.
Los cuadrados se caracterizan por tener cuatro lados de igual longitud y cuatro ángulos internos de 90 grados, lo que significa que sus lados son iguales en longitud y sus ángulos son iguales en medida.
P4.2.1.3: Algunos paralelogramos son romboides.
Los romboides tienen los lados opuestos que son paralelos entre sí, entonces nunca se cruzan y los lados adyacentes del romboide pueden tener longitudes diferentes, lo que hace que sus ángulos internos también sean diferentes.
P4.2.1.4: Algunos paralelogramos son rombos.
Los rombos son polígonos más específicamente son figuras planas que se forman a partir de una cantidad finita de segmentos rectos que aparecen dispuestos de manera consecutiva en un plano.
P4.2.2.1: Algunos cuadriláteros convexos son trapecios.
Los trapecios solo tiene dos lados paralelos entre sí, lo que nunca se cruzarán aún así se prolonguen. Dichos lados paralelos reciben el nombre de base mayor (B) y base menor (b).
P4.2.2.2: Algunos trapecios son trapecios escalenos.
Los trapecios escalenos tienen sus cuatro lados desiguales, siendo sus ángulos interiores siendo diferentes entre sí y no tiene un ángulo igual ni ángulo recto.
P4.2.2.3: Algunos trapecios son trapecios rectángulos.
Los trapecios rectángulos tiene dos ángulos rectos, uno agudo y otro obtuso. Puede tener dos lados iguales o todos distintos, también con sus uno o dos ángulos obtusos.
P4.2.3.1: Algunos cuadriláteros convexos son trapezoides.
Los trapezoides es una figura geométrica plana de 4 lados de los cuales ninguno es paralelo a otro, al ser prolongados, los segmentos que forman la figura podrían cruzarse.
P4.2.3.2: Algunos trapezoides son trapezoides sistemáticos.
Los trapezoides sistemáticos tiene dos pares de lados consecutivos iguales, que tiene un eje de simetría, sus diagonales son perpendiculares y se cruzan en el punto medio.
P4.2.3.3: Algunos trapezoides son trapezoides asimétricos.
Los trapezoides asimétricos tiene su lados no paralelos, ni un eje de simetría, entonces no son paralelogramos. Pero aún así sus ángulos internos al sumarlo da 360º.
Referencias
- Aguilar Durán, Rosa, & Inojosa, I. (2013). La geometría de los cuadriláteros en los libros de texto de educación primaria. Paradígma, 34(2), 151–173. http://ve.scielo.org/scielo.php?script=sci_arttext&pid=S1011-22512013000200009
- Smartick. (2016, April 4). Cuadriláteros: paralelogramos, trapecios y trapezoides | Smartick. Smartick. https://www.smartick.es/blog/matematicas/geometria/cuadrilateros/
- Westreicher, G. (2023). Cuadrilátero | Economipedia. Economipedia. https://economipedia.com/definiciones/cuadrilatero.html