Pseudomentefacto círculo

Pseudomentefacto círculo

---

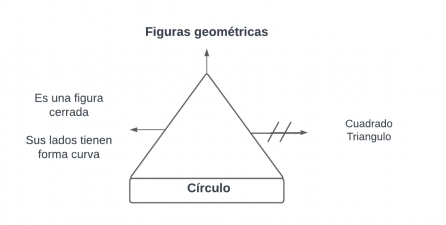
Paquete Proposicional

Supraordinada

Pp1.Todo circulo es una figura geométrica.

Isoordinadas

Pp2.1. Todo cirulo es una figura cerrada.

Pp2.2Todo circulo es una figura la cual todos sus lados tienen forma curva

Exclusiones

Pp3. Ningún circulo es cuadrado ni triangulo.

---

• Mentefactos proposicionales
• 

  Pp1.Todo circulo es una figura geométrica.

• 

  Pp2.1. Todo cirulo es una figura cerrada.

• 

  Pp2.2 Todo circulo es una figura la cual todos sus lados tienen forma curva

• 

  Pp3. Ningun circulo es cuadrado ni triangulo.

---

Argumentaciones

Pp.1 Todo círculo es una figura geométrica

El círculo es una figura plana que se define como el conjunto de todos los puntos en un plano que están a una distancia fija (el radio) de un punto fijo (el centro). Al ser una figura que se define mediante conceptos geométricos, es claramente una figura geométrica.

Pp.2.1. Todo círculo es una figura cerrada

El círculo es una figura cerrada porque es una curva que comienza y termina en el mismo punto, es decir, que su trayectoria no tiene principio ni fin. Esto implica que todo punto de la curva está contenido en la figura, lo que la hace una figura cerrada.

Pp.2.2. Todo círculo es una figura en la cual todos sus lados tienen forma curva

El círculo se define como una curva cerrada en la cual todos los puntos que la conforman están a la misma distancia del centro. Al ser una curva, todos los puntos de su borde tienen una forma curva, lo que implica que todos los lados de la figura también tienen una forma curva.

Pp.3 Ningún círculo es cuadrado ni triángulo

El círculo tiene propiedades geométricas diferentes a las del cuadrado y el triángulo. Por ejemplo, el círculo no tiene lados ni ángulos, lo que lo diferencia de ambas figuras. Además, el círculo no tiene vértices, que son puntos donde se unen dos o más lados en el caso del cuadrado y el triángulo. Por lo tanto, no puede ser cuadrado ni triángulo.