Diferencia entre revisiones de «Mentefacto Estadística»
(Agregación de marcos a los silogismos) |
(Retirar marcos) |
||
| Línea 29: | Línea 29: | ||
'''Argumentación:''' Dado que la estadística es una rama de la matemática aplicada que se dedica al análisis, recolección y estudio de datos para ofrecer información interpretada que sea relevante en una investigación. | '''Argumentación:''' Dado que la estadística es una rama de la matemática aplicada que se dedica al análisis, recolección y estudio de datos para ofrecer información interpretada que sea relevante en una investigación. | ||
[[Archivo:Silogismo aristotélico estadística - matemática.png|izquierda| | [[Archivo:Silogismo aristotélico estadística - matemática.png|izquierda|sinmarco]] | ||
| Línea 41: | Línea 41: | ||
'''Argumentación:''' Porque la estadística analiza conjuntos de datos, estos pueden ser en masa o pequeños, sin embargo, necesita un conjunto específico de de datos a analizar dependiendo de la investigación que se quiera hacer. | '''Argumentación:''' Porque la estadística analiza conjuntos de datos, estos pueden ser en masa o pequeños, sin embargo, necesita un conjunto específico de de datos a analizar dependiendo de la investigación que se quiera hacer. | ||
[[Archivo:Silogismo aristotélico estadística - análisis.png|izquierda| | [[Archivo:Silogismo aristotélico estadística - análisis.png|izquierda|sinmarco]] | ||
| Línea 54: | Línea 54: | ||
'''Argumentación:''' Ya que necesita orden al presentar los resultados obtenidos para que estos sean entendibles para el investigador y para el público en general, siendo así realmente útiles para futuras investigaciones. | '''Argumentación:''' Ya que necesita orden al presentar los resultados obtenidos para que estos sean entendibles para el investigador y para el público en general, siendo así realmente útiles para futuras investigaciones. | ||
[[Archivo:Silogismo aristotélico estadística - análisis de orden sistemático.png|izquierda| | [[Archivo:Silogismo aristotélico estadística - análisis de orden sistemático.png|izquierda|sinmarco]] | ||
| Línea 67: | Línea 67: | ||
'''Argumentación:''' Esto ya que al ser una rama de la matemática, el cálculo infinitesimal se encarga de facilitar resoluciones para los que la matemática tradicional era insuficiente, mientras que la estadística se dedica a analizar la probabilidad, la tendencia, media, etc, de un evento “x” o “y” que ocurra. | '''Argumentación:''' Esto ya que al ser una rama de la matemática, el cálculo infinitesimal se encarga de facilitar resoluciones para los que la matemática tradicional era insuficiente, mientras que la estadística se dedica a analizar la probabilidad, la tendencia, media, etc, de un evento “x” o “y” que ocurra. | ||
[[Archivo:Silogismo aristotélico estadística - cálculo infinitesimal.png|izquierda| | [[Archivo:Silogismo aristotélico estadística - cálculo infinitesimal.png|izquierda|sinmarco]] | ||
| Línea 81: | Línea 81: | ||
'''Argumentación:''' Pues la estadística se divide en dos grandes ramas, una de ellas es la estadística descriptiva, la cual se encarga de resumir la información contenida en los datos recogidos, a través de algunos métodos estadísticos como la desviación estándar, media, mediana, moda, etc. | '''Argumentación:''' Pues la estadística se divide en dos grandes ramas, una de ellas es la estadística descriptiva, la cual se encarga de resumir la información contenida en los datos recogidos, a través de algunos métodos estadísticos como la desviación estándar, media, mediana, moda, etc. | ||
[[Archivo:Silogismo aristotélico estadística - estadística descriptiva.png|izquierda| | [[Archivo:Silogismo aristotélico estadística - estadística descriptiva.png|izquierda|sinmarco]] | ||
| Línea 93: | Línea 93: | ||
'''Argumentación:''' Dado que describe la manera en la que se distribuyen los datos recogidos de la población seleccionada, facilitando la investigación. | '''Argumentación:''' Dado que describe la manera en la que se distribuyen los datos recogidos de la población seleccionada, facilitando la investigación. | ||
[[Archivo:Silogismo aristotélico estadística descriptiva - distribución de frecuencias.png|izquierda| | [[Archivo:Silogismo aristotélico estadística descriptiva - distribución de frecuencias.png|izquierda|sinmarco]] | ||
| Línea 105: | Línea 105: | ||
'''Argumentación:''' Porque analiza y describe a qué tienden las variables según los datos recogidos y analizados a través del uso de media, mediana y moda, las cuales conforman a su vez las medidas de tendencia central. | '''Argumentación:''' Porque analiza y describe a qué tienden las variables según los datos recogidos y analizados a través del uso de media, mediana y moda, las cuales conforman a su vez las medidas de tendencia central. | ||
[[Archivo:Silogismo aristotélico estadística descriptiva - medida de tendencia central.png|izquierda| | [[Archivo:Silogismo aristotélico estadística descriptiva - medida de tendencia central.png|izquierda|sinmarco]] | ||
| Línea 117: | Línea 117: | ||
'''Argumentación:''' Pues describe cuánto pueden variar los datos recogidos de la muestra analizada, esto a través del uso de la varianza, desviación estándar, cuartiles y el rango. | '''Argumentación:''' Pues describe cuánto pueden variar los datos recogidos de la muestra analizada, esto a través del uso de la varianza, desviación estándar, cuartiles y el rango. | ||
[[Archivo:Silogismo aristotélico estadística descriptiva - medida de variabilidad.png|izquierda| | [[Archivo:Silogismo aristotélico estadística descriptiva - medida de variabilidad.png|izquierda|sinmarco]] | ||
| Línea 129: | Línea 129: | ||
'''Argumentación:''' Dado que la estadística se divide en dos grandes ramas, una de ellas es la estadística inferencial, la cual se encarga de inferir métodos y procedimientos a través de la inducción, concluyendo y determinando propiedades de una población estadística a partir de una parte de la misma. | '''Argumentación:''' Dado que la estadística se divide en dos grandes ramas, una de ellas es la estadística inferencial, la cual se encarga de inferir métodos y procedimientos a través de la inducción, concluyendo y determinando propiedades de una población estadística a partir de una parte de la misma. | ||
[[Archivo:Silogismo aristotélico estadística - estadística inferencial.png|izquierda| | [[Archivo:Silogismo aristotélico estadística - estadística inferencial.png|izquierda|sinmarco]] | ||
| Línea 141: | Línea 141: | ||
'''Argumentación:''' Ya que esta rama de la estadística inferencial se ajusta a los llamados criterios paramétricos, entre los cuales hay: la media, y la desviación estándar, este método se vuelve recomendable cuando los datos se ajustan a una distribución conocida, independientemente de cuál sea. | '''Argumentación:''' Ya que esta rama de la estadística inferencial se ajusta a los llamados criterios paramétricos, entre los cuales hay: la media, y la desviación estándar, este método se vuelve recomendable cuando los datos se ajustan a una distribución conocida, independientemente de cuál sea. | ||
[[Archivo:Silogismo aristotélico estadística inferencial - estadística inferencial paramétrica.png|izquierda| | [[Archivo:Silogismo aristotélico estadística inferencial - estadística inferencial paramétrica.png|izquierda|sinmarco]] | ||
| Línea 153: | Línea 153: | ||
'''Argumentación:''' Porque esta rama de la estadística inferencial no se ajusta a los llamados criterios paramétricos, esta estudia las pruebas y modelos estadísticos, este método se vuelve recomendable cuando los datos no se ajustan a una distribución conocida. | '''Argumentación:''' Porque esta rama de la estadística inferencial no se ajusta a los llamados criterios paramétricos, esta estudia las pruebas y modelos estadísticos, este método se vuelve recomendable cuando los datos no se ajustan a una distribución conocida. | ||
[[Archivo:Silogismo aristotélico estadística inferencial - estadística inferencial no paramétrica.png|izquierda| | [[Archivo:Silogismo aristotélico estadística inferencial - estadística inferencial no paramétrica.png|izquierda|sinmarco]] | ||
Revisión del 02:47 20 may 2023
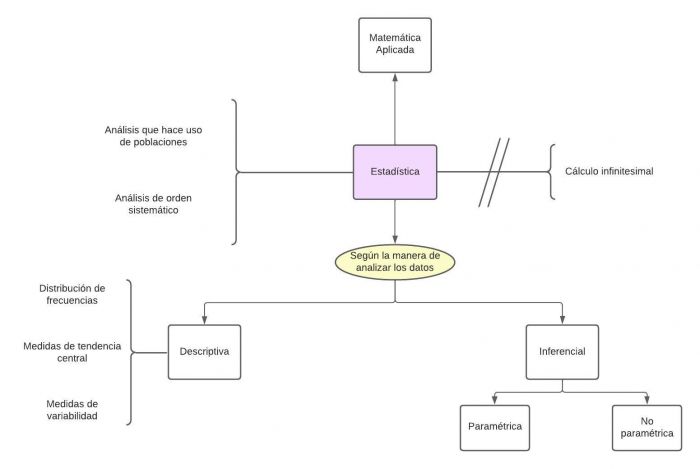
Estadística
Paquete proposicional
P1.- Toda estadística es matemática aplicada.
P2.1.- Toda estadística es análisis que hace uso de poblaciones.
P2.2.- Toda estadística es análisis de orden sistemático.
P3.- Ninguna estadística es cálculo infinitesimal
P4.1.- Alguna estadística, según la manera de analizar los datos, es descriptiva.
P4.1.1.- Toda estadística descriptiva es estadística que hace uso de distribución de frecuencias.
P4.1.2.- Toda estadística descriptiva es estadística que hace uso de medidas de tendencia central.
P4.1.3.- Toda estadística descriptiva es estadística que hace uso de medidas de variabilidad.
P4.2.- Alguna estadística, según la manera de analizar los datos, es inferencial.
P4.2.1.- Alguna estadística inferencial es paramétrica.
P4.2.2.- Alguna estadística inferencial es no paramétrica.
Argumento proposicional
P1.Toda estadística es matemática aplicada.
Argumentación: Dado que la estadística es una rama de la matemática aplicada que se dedica al análisis, recolección y estudio de datos para ofrecer información interpretada que sea relevante en una investigación.
P2.1.Toda estadística es análisis que hace uso de poblaciones.
Argumentación: Porque la estadística analiza conjuntos de datos, estos pueden ser en masa o pequeños, sin embargo, necesita un conjunto específico de de datos a analizar dependiendo de la investigación que se quiera hacer.
P2.2.Toda estadística es análisis de orden sistemático.
Argumentación: Ya que necesita orden al presentar los resultados obtenidos para que estos sean entendibles para el investigador y para el público en general, siendo así realmente útiles para futuras investigaciones.
P3.Ninguna estadística es cálculo infinitesimal.
Argumentación: Esto ya que al ser una rama de la matemática, el cálculo infinitesimal se encarga de facilitar resoluciones para los que la matemática tradicional era insuficiente, mientras que la estadística se dedica a analizar la probabilidad, la tendencia, media, etc, de un evento “x” o “y” que ocurra.
P4.1.Alguna estadística, según la manera de analizar los datos, es descriptiva.
Argumentación: Pues la estadística se divide en dos grandes ramas, una de ellas es la estadística descriptiva, la cual se encarga de resumir la información contenida en los datos recogidos, a través de algunos métodos estadísticos como la desviación estándar, media, mediana, moda, etc.
P4.1.1.Toda estadística descriptiva es estadística que hace uso de distribución de frecuencias.
Argumentación: Dado que describe la manera en la que se distribuyen los datos recogidos de la población seleccionada, facilitando la investigación.
P4.1.2.Toda estadística descriptiva es estadística que hace uso de medidas de tendencia central.
Argumentación: Porque analiza y describe a qué tienden las variables según los datos recogidos y analizados a través del uso de media, mediana y moda, las cuales conforman a su vez las medidas de tendencia central.
P4.1.3.Toda estadística descriptiva es estadística que hace uso de medidas de variabilidad.
Argumentación: Pues describe cuánto pueden variar los datos recogidos de la muestra analizada, esto a través del uso de la varianza, desviación estándar, cuartiles y el rango.
P4.2.Alguna estadística, según la manera de analizar los datos, es inferencial.
Argumentación: Dado que la estadística se divide en dos grandes ramas, una de ellas es la estadística inferencial, la cual se encarga de inferir métodos y procedimientos a través de la inducción, concluyendo y determinando propiedades de una población estadística a partir de una parte de la misma.
P4.2.1.Alguna estadística inferencial es paramétrica.
Argumentación: Ya que esta rama de la estadística inferencial se ajusta a los llamados criterios paramétricos, entre los cuales hay: la media, y la desviación estándar, este método se vuelve recomendable cuando los datos se ajustan a una distribución conocida, independientemente de cuál sea.
P4.2.2.Alguna estadística inferencial es no paramétrica.
Argumentación: Porque esta rama de la estadística inferencial no se ajusta a los llamados criterios paramétricos, esta estudia las pruebas y modelos estadísticos, este método se vuelve recomendable cuando los datos no se ajustan a una distribución conocida.
Link mentefacto Lucidchart:
References
Byju's (Ed.). (2017). Statistics Definition. Byju’s. https://byjus.com/maths/statistics-definition/#:~:text=Characteristics%20of%20Statistics&text=It%20has%20an%20aggregate%20of,collected%20for%20a%20planned%20purpose
Chappelow, J. (2023, March 25). Statistics in Math: Definition, Types, and Importance. Investopedia. https://www.investopedia.com/terms/s/statistics.asp#:~:text=Investopedia%20%2F%20Dennis%20Madamba-
Wikipedia. (2022, December 7). Statistics. Wikipedia. https://en.wikipedia.org/wiki/Statistics#:~:text=Statistics%20is%20a%20mathematical%20body
Durán, A. (2020, February 10). Cálculo infinitesimal. El lenguaje matemático de la naturaleza - Catarata. Www.catarata.org. https://www.catarata.org/libro/calculo-infinitesimal_117726/