Diferencia entre revisiones de «Mentefacto Función Exponencial»
(Creación total de mentefacto función exponencial) |
m (Cambiar el orden de los graficos y subtitulos ademas poner viñetas en las referencias) |
||
| Línea 1: | Línea 1: | ||
[[Archivo:Mentefacto funciones exponenciales.png|borde|centro|sinmarco|636x636px|Mentefacto conceptual de función exponencial ]] | [[Archivo:Mentefacto funciones exponenciales.png|borde|centro|sinmarco|636x636px|Mentefacto conceptual de función exponencial ]] | ||
=== '''<big>Paquete proposicional</big>''' === | |||
=== '''Supraordinada''' === | |||
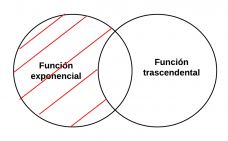
P1.- Toda función exponencial es función trascendental. | P1.- Toda función exponencial es función trascendental. | ||
=== Isoordinadas === | |||
P2.1.- Toda función exponencial es función de forma f(x)=ax. | P2.1.- Toda función exponencial es función de forma f(x)=ax. | ||
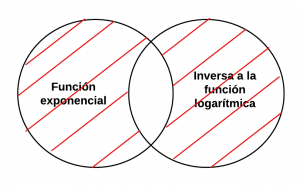
P2.2.- Toda función exponencial es inversa a la función logarítmica. | P2.2.- Toda función exponencial es inversa a la función logarítmica. | ||
=== Infraordinadas === | |||
P3.1.- Alguna función exponencial según su base posee base mayor que uno. | P3.1.- Alguna función exponencial según su base posee base mayor que uno. | ||
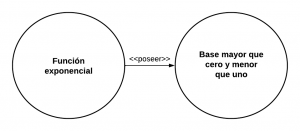
P3.2.- Alguna función exponencial según su base posee base mayor que cero y menor que uno. | P3.2.- Alguna función exponencial según su base posee base mayor que cero y menor que uno. | ||
=== Exclusiones === | |||
P4.1.- Ninguna función exponencial es función logarítmica. | P4.1.- Ninguna función exponencial es función logarítmica. | ||
| Línea 24: | Línea 24: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
! colspan=" | ! colspan="4" |'''Mentefactos proposicionales''' | ||
|- | |- | ||
|[[Archivo:Mentefacto Funciones Exponenciales - p1.png|alt=|izquierda|miniaturadeimagen|P1.- Toda función exponencial es función trascendental. ]] | |[[Archivo:Mentefacto Funciones Exponenciales - p1.png|alt=|izquierda|miniaturadeimagen|P1.- Toda función exponencial es función trascendental. |228x228px]] | ||
|[[Archivo:Mentefacto Funciones Exponenciales p2.1.png|miniaturadeimagen|P2.1.- Toda función exponencial es función de forma f(x)=ax.]] | |[[Archivo:Mentefacto Funciones Exponenciales p2.1.png|miniaturadeimagen|P2.1.- Toda función exponencial es función de forma f(x)=ax.|135x135px]] | ||
|[[Archivo:Mentefacto Funciones Exponenciales p2.2.png|miniaturadeimagen|P2.1.- Toda función exponencial es inversa a la función logarítmica.]] | |[[Archivo:Mentefacto Funciones Exponenciales p2.2.png|miniaturadeimagen|P2.1.- Toda función exponencial es inversa a la función logarítmica.]] | ||
|[[Archivo:Mentefacto Funciones Exponenciales P4.2.png|miniaturadeimagen|P3.2 .- Alguna función exponencial posee según su base base mayor que cero y menor que uno.]] | |[[Archivo:Mentefacto Funciones Exponenciales P4.2.png|miniaturadeimagen|P3.2 .- Alguna función exponencial posee según su base base mayor que cero y menor que uno.]] | ||
|[[Archivo:Mentefacto Funciones Exponenciales P4.1.png|miniaturadeimagen|P3.1.- Alguna función exponencial según su base posee base mayor que uno. ]] | |- | ||
|[[Archivo:Mentefacto Funciones Exponenciales P4.1.png|miniaturadeimagen|P3.1.- Alguna función exponencial según su base posee base mayor que uno. |256x256px]] | |||
|[[Archivo:Mentefacto Funciones Exponenciales P3.1.png|miniaturadeimagen|242x242px|P4.1.- Ninguna función exponencial es función logarítmica. ]] | |[[Archivo:Mentefacto Funciones Exponenciales P3.1.png|miniaturadeimagen|242x242px|P4.1.- Ninguna función exponencial es función logarítmica. ]] | ||
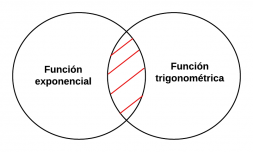
|[[Archivo:Mentefacto Funciones Exponenciales P3.2.png|miniaturadeimagen|253x253px|P4.2.- Ninguna función exponencial es función trigonométrica. ]] | |[[Archivo:Mentefacto Funciones Exponenciales P3.2.png|miniaturadeimagen|253x253px|P4.2.- Ninguna función exponencial es función trigonométrica. ]] | ||
| | |||
|} | |} | ||
==== '''<big>Argumentaciones</big>''' ==== | |||
==== P1.- Toda función exponencial es función trascendental. ==== | |||
Arg: La función exponencial es una función real de variable real, que posee una variable independiente que se expresa como un exponente o como el índice de una raíz. Como también puede ser afectada la función logarítmica o alguna de las funciones. | Arg: La función exponencial es una función real de variable real, que posee una variable independiente que se expresa como un exponente o como el índice de una raíz. Como también puede ser afectada la función logarítmica o alguna de las funciones. | ||
==== P2.1.- Toda función exponencial es función de forma f(x)=ax. ==== | |||
Arg: La constante al ser positiva y distinta de uno se debe a que la función exponencial se define como una función que relaciona un número base a con una potencia x. La base a es una constante positiva distinta de 1, y la potencia x es un número real cualquiera. | Arg: La constante al ser positiva y distinta de uno se debe a que la función exponencial se define como una función que relaciona un número base a con una potencia x. La base a es una constante positiva distinta de 1, y la potencia x es un número real cualquiera. | ||
==== P2.1.- Toda función exponencial es inversa a la función logarítmica. ==== | |||
Arg:La función exponencial se define como f(x) = a^x, donde a es una constante positiva diferente de 1, y x es cualquier número real. La función logarítmica inversa se define como g(x) = log a(x), donde a es la misma constante positiva diferente de 1. | Arg:La función exponencial se define como f(x) = a^x, donde a es una constante positiva diferente de 1, y x es cualquier número real. La función logarítmica inversa se define como g(x) = log a(x), donde a es la misma constante positiva diferente de 1. | ||
Si aplicamos la función exponencial a un número x, obtenemos a^x. Si aplicamos la función logarítmica inversa a a^x, obtenemos log a(a^x), que es igual a x. | Si aplicamos la función exponencial a un número x, obtenemos a^x. Si aplicamos la función logarítmica inversa a a^x, obtenemos log a(a^x), que es igual a x. | ||
==== P3.1.- Ninguna función exponencial es función logarítmica. ==== | |||
Arg: Una función logarítmica es una función de la forma g(x) = loga(x) , donde a es una constante positiva distinta de 1 y “x” es un número real positivo. | Arg: Una función logarítmica es una función de la forma g(x) = loga(x) , donde a es una constante positiva distinta de 1 y “x” es un número real positivo. | ||
Es importante notar que las funciones exponenciales y logarítmicas son funciones inversas una de la otra. Esto significa que si tenemos una función exponencial f(x) = ax y una función logarítmica g(x) = loga(x), entonces la resultante de la fusión de las dos funciones es para todo x en el dominio de las funciones. | Es importante notar que las funciones exponenciales y logarítmicas son funciones inversas una de la otra. Esto significa que si tenemos una función exponencial f(x) = ax y una función logarítmica g(x) = loga(x), entonces la resultante de la fusión de las dos funciones es para todo x en el dominio de las funciones. | ||
==== P3.2.- Ninguna función exponencial es función trigonométrica. ==== | |||
Arg: Una función trigonométrica es una función que relaciona un ángulo con un valor trigonométrico (como el seno, el coseno o la tangente) de ese ángulo. | Arg: Una función trigonométrica es una función que relaciona un ángulo con un valor trigonométrico (como el seno, el coseno o la tangente) de ese ángulo. | ||
Las funciones exponenciales crecen o decrecen de manera exponencial a medida que el valor de x aumenta o disminuye, mientras que las funciones trigonométricas son periódicas y tienen una forma de onda repetitiva. | Las funciones exponenciales crecen o decrecen de manera exponencial a medida que el valor de x aumenta o disminuye, mientras que las funciones trigonométricas son periódicas y tienen una forma de onda repetitiva. | ||
==== P4.1.- Alguna función exponencial según su base posee base mayor que uno. ==== | |||
Arg: Recordando que la base de una función exponencial es el valor de a, la base a es mayor que uno, entonces la función exponencial crece de manera exponencial a medida que el valor de x aumenta. Por ejemplo, la función exponencial f(x) = 2^x tiene una base igual a 2, y crece de manera exponencial a medida que x aumenta. | Arg: Recordando que la base de una función exponencial es el valor de a, la base a es mayor que uno, entonces la función exponencial crece de manera exponencial a medida que el valor de x aumenta. Por ejemplo, la función exponencial f(x) = 2^x tiene una base igual a 2, y crece de manera exponencial a medida que x aumenta. | ||
==== P4.2 .- Alguna función exponencial posee según su base base mayor que cero y menor que uno. ==== | |||
Arg: Si la base es mayor que cero, la función exponencial siempre será positiva o creciente, mientras que si la base es menor que uno, la función exponencial siempre será positiva o decreciente. | Arg: Si la base es mayor que cero, la función exponencial siempre será positiva o creciente, mientras que si la base es menor que uno, la función exponencial siempre será positiva o decreciente. | ||
===== '''<big>Referencias</big>''' ===== | |||
CULTURAL, S. A. Aritmética. 1994. Madrid España, CULTURAL, S. A, 1994, pp. 110–112. | * Guinjoan, Marc. “Iniciación a Las Matemáticas Para La Ingeniería .” UOC, cimanet.uoc.edu/cursMates0/IniciacionMatematicas/s9/2_4_3.html#:~:text=La%20funci%C3%B3n%20exponencial%20y%20la,vida%20cotidiana%20por%20sus%20aplicaciones. Accessed 21 Apr. 2023. | ||
* “FUNCIONES Y ECUACIONES EXPONENCIALES Y LOGARÍTMICAS.” Inline, www.educ.ar/recursos/151217/funciones-y-ecuaciones-exponenciales-y-logaritmicas/download/inline#:~:text=La%20f%C3%B3rmula%20gen%C3%A9rica%20de%20la,y%20admite%20cualquier%20valor%20real. Accessed 20 Apr. 2023. | |||
* “Funciones Trigonométricas.” TodaMateria, 2012, www.todamateria.com/funciones-trigonometricas/. Accessed 20 Apr. 2023. | |||
* Perez, Eduardo . “Función Logarítmica .” Universo Formulas, 30 Nov. 2020, www.universoformulas.com/matematicas/analisis/funcion-logaritmica/. Accessed 20 Apr. 2023. | |||
* CULTURAL, S. A. Aritmética. 1994. Madrid España, CULTURAL, S. A, 1994, pp. 110–112. | |||
Revisión del 23:06 19 may 2023
Paquete proposicional
Supraordinada
P1.- Toda función exponencial es función trascendental.
Isoordinadas
P2.1.- Toda función exponencial es función de forma f(x)=ax.
P2.2.- Toda función exponencial es inversa a la función logarítmica.
Infraordinadas
P3.1.- Alguna función exponencial según su base posee base mayor que uno.
P3.2.- Alguna función exponencial según su base posee base mayor que cero y menor que uno.
Exclusiones
P4.1.- Ninguna función exponencial es función logarítmica.
P4.2.- Ninguna función exponencial es función trigonométrica.
| Mentefactos proposicionales | |||
|---|---|---|---|
Argumentaciones
P1.- Toda función exponencial es función trascendental.
Arg: La función exponencial es una función real de variable real, que posee una variable independiente que se expresa como un exponente o como el índice de una raíz. Como también puede ser afectada la función logarítmica o alguna de las funciones.
P2.1.- Toda función exponencial es función de forma f(x)=ax.
Arg: La constante al ser positiva y distinta de uno se debe a que la función exponencial se define como una función que relaciona un número base a con una potencia x. La base a es una constante positiva distinta de 1, y la potencia x es un número real cualquiera.
P2.1.- Toda función exponencial es inversa a la función logarítmica.
Arg:La función exponencial se define como f(x) = a^x, donde a es una constante positiva diferente de 1, y x es cualquier número real. La función logarítmica inversa se define como g(x) = log a(x), donde a es la misma constante positiva diferente de 1.
Si aplicamos la función exponencial a un número x, obtenemos a^x. Si aplicamos la función logarítmica inversa a a^x, obtenemos log a(a^x), que es igual a x.
P3.1.- Ninguna función exponencial es función logarítmica.
Arg: Una función logarítmica es una función de la forma g(x) = loga(x) , donde a es una constante positiva distinta de 1 y “x” es un número real positivo.
Es importante notar que las funciones exponenciales y logarítmicas son funciones inversas una de la otra. Esto significa que si tenemos una función exponencial f(x) = ax y una función logarítmica g(x) = loga(x), entonces la resultante de la fusión de las dos funciones es para todo x en el dominio de las funciones.
P3.2.- Ninguna función exponencial es función trigonométrica.
Arg: Una función trigonométrica es una función que relaciona un ángulo con un valor trigonométrico (como el seno, el coseno o la tangente) de ese ángulo.
Las funciones exponenciales crecen o decrecen de manera exponencial a medida que el valor de x aumenta o disminuye, mientras que las funciones trigonométricas son periódicas y tienen una forma de onda repetitiva.
P4.1.- Alguna función exponencial según su base posee base mayor que uno.
Arg: Recordando que la base de una función exponencial es el valor de a, la base a es mayor que uno, entonces la función exponencial crece de manera exponencial a medida que el valor de x aumenta. Por ejemplo, la función exponencial f(x) = 2^x tiene una base igual a 2, y crece de manera exponencial a medida que x aumenta.
P4.2 .- Alguna función exponencial posee según su base base mayor que cero y menor que uno.
Arg: Si la base es mayor que cero, la función exponencial siempre será positiva o creciente, mientras que si la base es menor que uno, la función exponencial siempre será positiva o decreciente.
Referencias
- Guinjoan, Marc. “Iniciación a Las Matemáticas Para La Ingeniería .” UOC, cimanet.uoc.edu/cursMates0/IniciacionMatematicas/s9/2_4_3.html#:~:text=La%20funci%C3%B3n%20exponencial%20y%20la,vida%20cotidiana%20por%20sus%20aplicaciones. Accessed 21 Apr. 2023.
- “FUNCIONES Y ECUACIONES EXPONENCIALES Y LOGARÍTMICAS.” Inline, www.educ.ar/recursos/151217/funciones-y-ecuaciones-exponenciales-y-logaritmicas/download/inline#:~:text=La%20f%C3%B3rmula%20gen%C3%A9rica%20de%20la,y%20admite%20cualquier%20valor%20real. Accessed 20 Apr. 2023.
- “Funciones Trigonométricas.” TodaMateria, 2012, www.todamateria.com/funciones-trigonometricas/. Accessed 20 Apr. 2023.
- Perez, Eduardo . “Función Logarítmica .” Universo Formulas, 30 Nov. 2020, www.universoformulas.com/matematicas/analisis/funcion-logaritmica/. Accessed 20 Apr. 2023.
- CULTURAL, S. A. Aritmética. 1994. Madrid España, CULTURAL, S. A, 1994, pp. 110–112.