Diferencia entre revisiones de «Pseudomentefacto Números Naturales»
(Realizar las argumentaciones y los mentefactos) |
(Añadi las referencias) |
||
| Línea 58: | Línea 58: | ||
Porque los números negativos son aquellos que se expresan con el signo menos (-) a la izquierda y su valor es menor que cero (0) mientras que los números naturales son infinitos positivos que van a la derecha de cero. | Porque los números negativos son aquellos que se expresan con el signo menos (-) a la izquierda y su valor es menor que cero (0) mientras que los números naturales son infinitos positivos que van a la derecha de cero. | ||
----'''<big>Referencias</big>''' | ----'''<big>Referencias</big>''' | ||
de, Colaboradores. “Número Usado Para Contar Los Elementos de Un Conjunto.” ''Wikipedia.org'', Wikimedia Foundation, Inc., 10 Feb. 2002, https://es.wikipedia.org/wiki/N%C3%BAmero_natural | |||
Revisión del 23:08 21 abr 2023
Paquete Proposicional
Supraordinadas
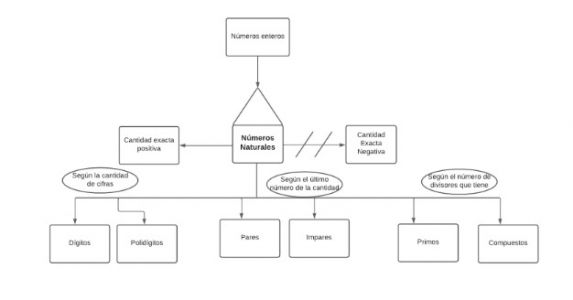
P1. Todos los números naturales son números enteros.
Isoordinadas
P2.Todo número natural es cantidad exacta positiva.
Infraordinadas
P3.1. Algunos números naturales, según su cantidad de cifras, son dígitos y polidígitos.
P3.2. Algunos números naturales, según el número final de la cantidad, son pares e impares.
P3.3. Algunos números naturales, según número de divisores que tienen, son números primos y números compuestos.
Exclusiones
P4. Ningún Número Natural es cantidad exacta negativa.
Mentefactos Proposicionales
P1: Todos los números naturales son números enteros.
P2:Todo número natural es cantidad exacta positiva.
P3.1: Algunos números naturales, según su cantidad de cifras, son dígitos y polidígitos.
P3.2: Algunos números naturales, según el número final de la cantidad, son pares e impares.
P3.3: Algunos números naturales, según número de divisores que tienen, son números primos y números compuestos.
P4: Ningún Número Natural es cantidad exacta negativa.
Argumentaciones
P1. Todos los números naturales son números enteros.
Porque los números naturales son infinitos y sirven para contar mientras que los números enteros son aquellos positivos y negativos incluido el cero y no tienen parte decimal. El número natural forma parte de este grupo de números enteros.
P2.Todo número natural es cantidad exacta positiva.
Porque estos números hacen referencia a aquellos que no tienen fin, estos son considerados infinitos porque se trata de una sucesión que no tiene límite, en matemáticas el infinito se representa con “∞” y no es medible, además de permitir representar la cantidad de elementos que tiene un conjunto.
P3.1. Algunos números naturales, según su cantidad de cifras, son dígitos y polidígitos.
Porque los dígitos son números formados por una cifra y los polidígitos están formados por dos o más cifras, esta clasificación es muy importante para el análisis de los números naturales y sus grandes conceptos que posee.
P3.2. Algunos números naturales, según el número final de la cantidad, son pares e impares.
Porque existen distintas clasificaciones de los números naturales, una de estas es la de los pares e impares donde los pares se reconocen como las cantidades que terminan en 0,2,4,6,8 y los impares se les conoce como las cantidades que terminan en 1,3,5,7,9.
P3.3. Algunos números naturales, según número de divisores que tienen, son números primos y números compuestos.
Porque los números primos son aquellos que tienen dos divisores, la unidad y ellos mismos y los números compuestos que son aquellos que tienen tres o más divisores, cumplen con características diferentes a las demás clasificaciones y es importante reconocerlo.
P4. Ningún Número Natural es cantidad exacta negativa.
Porque los números negativos son aquellos que se expresan con el signo menos (-) a la izquierda y su valor es menor que cero (0) mientras que los números naturales son infinitos positivos que van a la derecha de cero.
Referencias
de, Colaboradores. “Número Usado Para Contar Los Elementos de Un Conjunto.” Wikipedia.org, Wikimedia Foundation, Inc., 10 Feb. 2002, https://es.wikipedia.org/wiki/N%C3%BAmero_natural