Diferencia entre revisiones de «Pseudomentefacto Números Impares»
(Paquete Proposicional - Argumentaciones) |
(Pseudomentefacto - Mentefactos Proposicionales) |
||
| Línea 1: | Línea 1: | ||
[[Archivo:Pseudomentefacto de numeros impares.jpg|centro|miniaturadeimagen|684x684px|Pseudomentefacto Números Impares]] | |||
---- | ---- | ||
| Línea 8: | Línea 9: | ||
'''Isoordinadas:''' | '''Isoordinadas:''' | ||
P2.1: | P2.1: Ningún número impar es divisor de dos. | ||
P2.2 | P2.2: Todo número impar es el número que termina en 1 - 3 - 5 - 7 o 9. | ||
'''Exclusiones:''' | '''Exclusiones:''' | ||
P3: Ningún número impar es número par. | P3: Ningún número impar es número par. | ||
----Mentefacto Proposicional | ----Mentefacto Proposicional<gallery> | ||
Archivo:Mentefacto proposicion 1.png|P1: Todo número impar es número natural. | |||
Archivo:Mentefacto proposicion 2.2.png|P2.1: Ningún número impar es divisor de dos. | |||
Archivo:Mentefacto proposicion 2.1.png|P2.2: Todo número impar es el número que termina en 1 - 3 - 5 - 7 o 9. | |||
Archivo:Mentefacto proposicion 3 exclusion.png|P3: Ningún número impar es número par. | |||
</gallery> | |||
---- | ---- | ||
| Línea 25: | Línea 29: | ||
Argumento: Porque los números naturales son los números que se pueden contar y además son infinitos, las mismas características que tienen los impares. | Argumento: Porque los números naturales son los números que se pueden contar y además son infinitos, las mismas características que tienen los impares. | ||
'''P2.1 | '''P2.1: Ningún número impar es divisor de dos.''' | ||
Argumento: Porque los números impares al dividirlo para dos no sale 0 o un número natural completo, el resultado de esa división daría un número decimal. | Argumento: Porque los números impares al dividirlo para dos no sale 0 o un número natural completo, el resultado de esa división daría un número decimal. | ||
'''P2. | '''P2.2: Todo número impar es el número que termina en 1 - 3 - 5 - 7 o 9.''' | ||
Argumento: Porque | Argumento: Porque los números impares no son múltiplos de 2, por lo tanto, su última cifra siempre será 1 - 3 - 5 - 7 - 9. | ||
'''P3: Ningún número impar es número par.''' | '''P3: Ningún número impar es número par.''' | ||
Argumento: Porque el número impar son los números que terminan en 1 - 3 - 5 - 7 - 9 además no son divisibles ni múltiplos de dos, en cambio, los números pares son los números que terminan en 0 - 2 - 4 - 6 - 8 y si son divisibles o múltiplos de dos. | Argumento: Porque el número impar son los números que terminan en 1 - 3 - 5 - 7 - 9 además no son divisibles ni múltiplos de dos, en cambio, los números pares son los números que terminan en 0 - 2 - 4 - 6 - 8 y si son divisibles o múltiplos de dos. | ||
----Referencias | |||
Revisión del 22:48 20 abr 2023
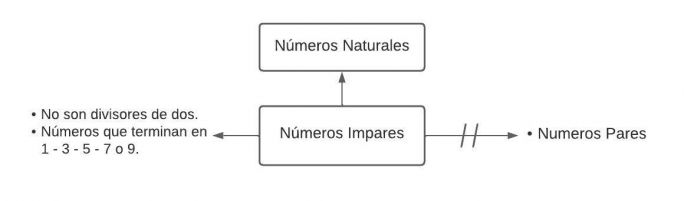
Paquete Proposicional
Supraordinada:
P1: Todo número impar es número natural.
Isoordinadas:
P2.1: Ningún número impar es divisor de dos.
P2.2: Todo número impar es el número que termina en 1 - 3 - 5 - 7 o 9.
Exclusiones:
P3: Ningún número impar es número par.
Mentefacto Proposicional
P1: Todo número impar es número natural.
P2.1: Ningún número impar es divisor de dos.
P2.2: Todo número impar es el número que termina en 1 - 3 - 5 - 7 o 9.
P3: Ningún número impar es número par.
Argumentaciones
P1: Todo número impar es número natural.
Argumento: Porque los números naturales son los números que se pueden contar y además son infinitos, las mismas características que tienen los impares.
P2.1: Ningún número impar es divisor de dos.
Argumento: Porque los números impares al dividirlo para dos no sale 0 o un número natural completo, el resultado de esa división daría un número decimal.
P2.2: Todo número impar es el número que termina en 1 - 3 - 5 - 7 o 9.
Argumento: Porque los números impares no son múltiplos de 2, por lo tanto, su última cifra siempre será 1 - 3 - 5 - 7 - 9.
P3: Ningún número impar es número par.
Argumento: Porque el número impar son los números que terminan en 1 - 3 - 5 - 7 - 9 además no son divisibles ni múltiplos de dos, en cambio, los números pares son los números que terminan en 0 - 2 - 4 - 6 - 8 y si son divisibles o múltiplos de dos.
Referencias