Diferencia entre revisiones de «Mentefacto intersección conjuntos»
m (Correción imágenes) |
m (Revisión ortográfica.) |
||
| (No se muestran 2 ediciones intermedias de 2 usuarios) | |||
| Línea 37: | Línea 37: | ||
'''''P1.- Toda intersección de conjuntos es operación entre conjuntos.''''' | '''''P1.- Toda intersección de conjuntos es operación entre conjuntos.''''' | ||
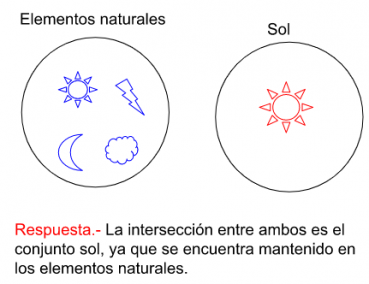
''<u>Argumentación.-</u>'' Porque la intersección de conjuntos es una operación que se puede realizar entre | ''<u>Argumentación.-</u>'' Porque la intersección de conjuntos es una operación que se puede realizar entre varios conjuntos o intervalos (abiertos, cerrados, semiabiertos, infinitos o universales). La cuál nos da como resultado todos los valores comunes entre los conjuntos en los que se realiza la operación. Es decir, la intersección es una operación que te da como resultado un conjunto que se rige a las propiedades de la operación realizada, entre las cuales tenemos: asociativa "<math>A\cap (B\cap C)=(A \cap B)\cap C</math>", conmutativa "<math>B\cap C=C \cap B</math>", indempotencia "<math>A\cap A=A</math>", universalidad "<math>R\cap A=A</math>" y conjunto vacío "<math>C\cap \varnothing=\varnothing</math>".[[Archivo:Ejemplo3 interseccion.png|centro|miniaturadeimagen|369x369px|Intersección de conjuntos.]]'''P2.1.- Toda intersección de conjuntos es operación que da un conjunto solución con los elementos comunes entre 2 o más conjuntos.''' | ||
''<u>Argumentación.-</u>'' Porque la intersección de conjuntos es una operación que se puede realizar entre varios conjuntos, la cual tiene como objetivo encontrar los elementos comunes entre estos, pero, no siempre existirá | ''<u>Argumentación.-</u>'' Porque la intersección de conjuntos es una operación que se puede realizar entre varios conjuntos, la cual tiene como objetivo encontrar los elementos comunes entre estos, pero, no siempre existirá una respuesta (conjunto vacío) o dará como respuesta un conjunto universal. Esta al igual que, las otras operaciones y las propiedades de las inecuaciones, nos ayudarán a resolver inecuaciones puesto que en la misma se usan signos como mayor o menor que, en vez del igual (ecuaciones). | ||
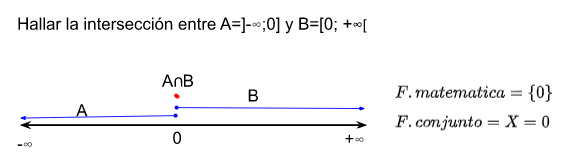
[[Archivo:Ejemplo4 interseccion.png|centro|miniaturadeimagen|562x562px|Intervalo con intersección igual a 0]] | [[Archivo:Ejemplo4 interseccion.png|centro|miniaturadeimagen|562x562px|Intervalo con intersección igual a 0]] | ||
'''''P2.2.- Toda intersección de conjuntos es operación que se le representa con el símbolo "∩".''''' | '''''P2.2.- Toda intersección de conjuntos es operación que se le representa con el símbolo "∩".''''' | ||
''<u>Argumentación.-</u>'' Porque | ''<u>Argumentación.-</u>'' Porque en todos los casos usamos el símbolo "∩" para referirnos que estamos realizando una intersección y no confundirnos con las otras operaciones de conjuntos que existen; como: la unión, intersección y complemento. Pero, si hablamos de intersección de intervalos, se la puede representar de forma: geométrica, matemática y de conjunto. En el caso de la forma geométrica, se utiliza una recta que va desde menos infinito hasta más infinito, mientras que, en el caso de la forma de conjunto se utiliza los corchete abierto y cerrados dependiendo del caso. Por otro lado, en la forma matemática se utilizan los símbolos "<math>\leq,<,>,\geq</math>" , donde se usa mayor igual o menor igual cuando el extremo del conjunto solución es cerrado, mientras que, se usa mayor o menor que cuando el extremo del conjunto solución es abierto. | ||
[[Archivo:Ejemplo2 interseccion.png|centro|miniaturadeimagen|615x615px|Intervalo con intersección semiabierta.]] | [[Archivo:Ejemplo2 interseccion.png|centro|miniaturadeimagen|615x615px|Intervalo con intersección semiabierta.]] | ||
| Línea 50: | Línea 50: | ||
''<u>Argumentación.-</u>'' Porque la unión te da un conjunto solución con todos los elementos comunes o no comunes entre 2 o más conjuntos. Es decir, la unión es aquella operación que une al conjunto A y B sin incluir a los elementos fuera de estos. | ''<u>Argumentación.-</u>'' Porque la unión te da un conjunto solución con todos los elementos comunes o no comunes entre 2 o más conjuntos. Es decir, la unión es aquella operación que une al conjunto A y B sin incluir a los elementos fuera de estos. | ||
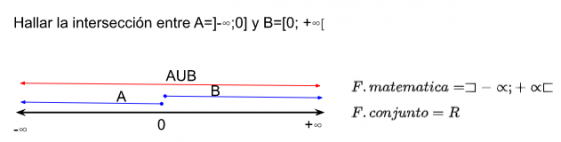
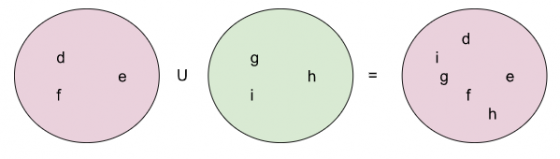
[[Archivo:Ejemplo1 interseccion.png|centro|miniaturadeimagen| | [[Archivo:Ejemplo1 interseccion.png|centro|miniaturadeimagen|561x561px|Intervalo de unión. [[Archivo:Mentefaco U.png|560x560px]]Unión de conjuntos.]] | ||
'''''P3.2.- Ninguna intersección de conjuntos es diferencia.''''' | '''''P3.2.- Ninguna intersección de conjuntos es diferencia.''''' | ||
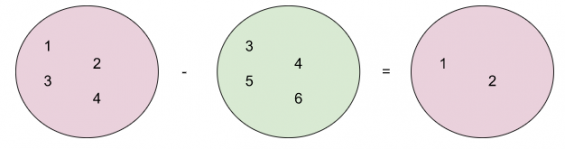
<u>Argumentación.-</u> Porque la diferencia te da un conjunto solución con todos los elementos del minuendo (primer conjunto) que no pertenecen al o los sustraendos (segundo conjunto o más). Por ejemplo, si el conjunto A contiene manzanas y plátanos, mientras que, el conjunto B contiene manzanas; la diferencia sería | <u>Argumentación.-</u> Porque la diferencia te da un conjunto solución con todos los elementos del minuendo (primer conjunto) que no pertenecen al o los sustraendos (segundo conjunto o más). Por ejemplo, si el conjunto A contiene manzanas y plátanos, mientras que, el conjunto B contiene manzanas; la diferencia sería plátanos. | ||
[[Archivo:Ejemplo diferencia.png|centro|miniaturadeimagen|563x563px|Intervalo de diferencia entre conjuntos]] | [[Archivo:Ejemplo diferencia.png|centro|miniaturadeimagen|563x563px|Intervalo de diferencia.[[Archivo:Mentefacto diferencia.png|565x565px]]Diferencia entre conjuntos.]] | ||
'''''P3.3.- Ninguna intersección de conjuntos es complemento.''''' | '''''P3.3.- Ninguna intersección de conjuntos es complemento.''''' | ||
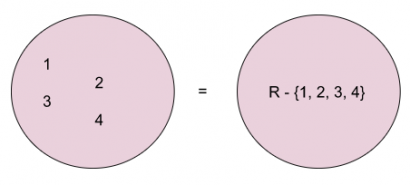
<u>Argumentación.-</u> Porque el complemento te da un conjunto solución con todos los elementos que no pertenecen a un conjunto cualesquiera. Está operación se caracteriza por realizarse con un solo conjunto, donde, los extremos | <u>Argumentación.-</u> Porque el complemento te da un conjunto solución con todos los elementos que no pertenecen a un conjunto cualesquiera. Está operación se caracteriza por realizarse con un solo conjunto, donde, si hablamos de intervalos los extremos cambian al contrario. Por ejemplo, si un extremo de un intervalo es cerrado en la solución ese extremo sería abierto, y así viceversa. | ||
[[Archivo:Ejemplo complemento.png|centro|miniaturadeimagen|561x561px|Intervalo de complemento de un conjunto.]] | [[Archivo:Ejemplo complemento.png|centro|miniaturadeimagen|561x561px|Intervalo de complemento.[[Archivo:Mentefacto complemento.png|centro|410x410px]]Complemento de un conjunto.]] | ||
---- | ---- | ||
Revisión actual - 12:47 20 abr 2023
Paquete proposicional.-
Supraordinada:
P1.- Toda intersección de conjuntos es operación entre conjuntos.
Isoordinadas:
P2.1.- Toda intersección de conjuntos es operación que da un conjunto solución con los elementos comunes entre 2 o más conjuntos.
P2.2.- Toda intersección de conjuntos es operación que se le representa con el símbolo "∩".
Exclusión:
P3.1.- Ninguna intersección de conjuntos es unión.
P3.2.- Ninguna intersección de conjuntos es diferencia.
P3.3.- Ninguna intersección de conjuntos es complemento.
Mentefactos proposicionales.-
Argumentaciones.-
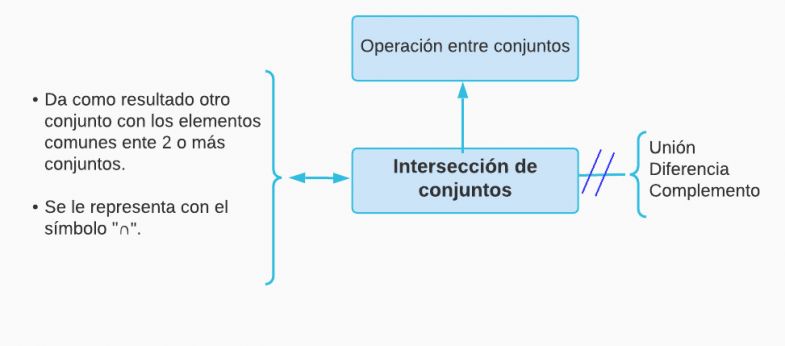
P1.- Toda intersección de conjuntos es operación entre conjuntos.
Argumentación.- Porque la intersección de conjuntos es una operación que se puede realizar entre varios conjuntos o intervalos (abiertos, cerrados, semiabiertos, infinitos o universales). La cuál nos da como resultado todos los valores comunes entre los conjuntos en los que se realiza la operación. Es decir, la intersección es una operación que te da como resultado un conjunto que se rige a las propiedades de la operación realizada, entre las cuales tenemos: asociativa "", conmutativa "", indempotencia "", universalidad "" y conjunto vacío "".
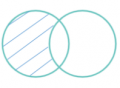
P2.1.- Toda intersección de conjuntos es operación que da un conjunto solución con los elementos comunes entre 2 o más conjuntos.
Argumentación.- Porque la intersección de conjuntos es una operación que se puede realizar entre varios conjuntos, la cual tiene como objetivo encontrar los elementos comunes entre estos, pero, no siempre existirá una respuesta (conjunto vacío) o dará como respuesta un conjunto universal. Esta al igual que, las otras operaciones y las propiedades de las inecuaciones, nos ayudarán a resolver inecuaciones puesto que en la misma se usan signos como mayor o menor que, en vez del igual (ecuaciones).
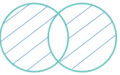
P2.2.- Toda intersección de conjuntos es operación que se le representa con el símbolo "∩".
Argumentación.- Porque en todos los casos usamos el símbolo "∩" para referirnos que estamos realizando una intersección y no confundirnos con las otras operaciones de conjuntos que existen; como: la unión, intersección y complemento. Pero, si hablamos de intersección de intervalos, se la puede representar de forma: geométrica, matemática y de conjunto. En el caso de la forma geométrica, se utiliza una recta que va desde menos infinito hasta más infinito, mientras que, en el caso de la forma de conjunto se utiliza los corchete abierto y cerrados dependiendo del caso. Por otro lado, en la forma matemática se utilizan los símbolos "" , donde se usa mayor igual o menor igual cuando el extremo del conjunto solución es cerrado, mientras que, se usa mayor o menor que cuando el extremo del conjunto solución es abierto.
P3.1.- Ninguna intersección de conjuntos es unión.
Argumentación.- Porque la unión te da un conjunto solución con todos los elementos comunes o no comunes entre 2 o más conjuntos. Es decir, la unión es aquella operación que une al conjunto A y B sin incluir a los elementos fuera de estos.
P3.2.- Ninguna intersección de conjuntos es diferencia.
Argumentación.- Porque la diferencia te da un conjunto solución con todos los elementos del minuendo (primer conjunto) que no pertenecen al o los sustraendos (segundo conjunto o más). Por ejemplo, si el conjunto A contiene manzanas y plátanos, mientras que, el conjunto B contiene manzanas; la diferencia sería plátanos.
P3.3.- Ninguna intersección de conjuntos es complemento.
Argumentación.- Porque el complemento te da un conjunto solución con todos los elementos que no pertenecen a un conjunto cualesquiera. Está operación se caracteriza por realizarse con un solo conjunto, donde, si hablamos de intervalos los extremos cambian al contrario. Por ejemplo, si un extremo de un intervalo es cerrado en la solución ese extremo sería abierto, y así viceversa.
Referencias bibliográficas.-
- Academia Internet. (2019, September 30). Interseccion de conjuntos ejercicios resueltos. Www.youtube.com. https://www.youtube.com/watch?v=r9q4O1uEn4w
- Alex, P. (2008, November 12). Intersección de conjuntos. Www.youtube.com. https://www.youtube.com/watch?v=2OSlnP8Ki6k
- Colaboradores de los proyectos Wikimedia. (2004, September 24). concepto en teoría de conjuntos. Wikipedia.org; Wikimedia Foundation, Inc. https://es.wikipedia.org/wiki/Intersecci%C3%B3n_de_conjuntos
- Martínez, G. O. C. (2021, September 20). Álgebra Superior I: Intersecciones, uniones y complementos de conjuntos. El Blog de Leo. https://blog.nekomath.com/algebra-superior-i-ntersecciones-uniones-y-complementos-de-conjuntos/