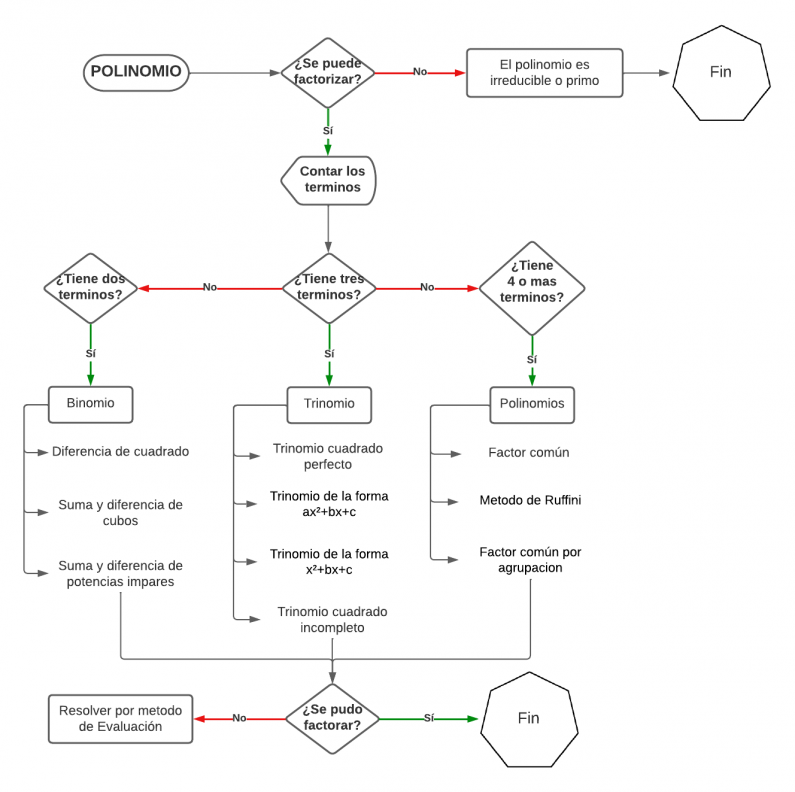
Flujograma Factorización

PROCESO: Identificar el tipo de factorización: Hay diferentes tipos de factorización que se pueden utilizar según el tipo de polinomio que se esté factorizando. Algunos de los métodos más comunes son la factorización por agrupación, la factorización por factor común, la factorización por diferencia de cuadrados, la factorización por suma y diferencia de cubos, y la factorización de polinomios cuadráticos. Encontrar factores comunes: Si el polinomio tiene términos comunes, se pueden factorizar utilizando la factorización por factor común. Encuentra el factor común de todos los términos del polinomio. Dividir cada término por el factor común para obtener la expresión simplificada. Escribe el factor común fuera de los paréntesis y escribe la expresión simplificada dentro de los paréntesis. Factorización por factor común por agrupación: Si el polinomio tiene cuatro términos Agrupa los términos del polinomio en dos grupos, de tal manera que cada grupo tenga al menos un factor común. Factoriza el factor común de cada grupo. Escribe el factor común fuera de los paréntesis y escribe la expresión simplificada dentro de los paréntesis. Si es posible, factoriza aún más los términos dentro de los paréntesis utilizando el método del factor común. Factorización de polinomios cuadráticos: Para factorizar un polinomio cuadrático de la forma ax^2 + bx + c, donde a, b, y c son coeficientes numéricos, sigue los siguientes pasos: Verifica si el polinomio se puede factorizar utilizando la técnica de factorización por inspección, es decir, buscando dos números que sumados den como resultado b y multiplicados den como resultado ac. Si encuentras estos números, entonces puedes factorizar el polinomio utilizando la fórmula (mx + r)(nx + s) = 0, donde m y n son los coeficientes del término cuadrático, r y s son los coeficientes del término constante y x es la variable. Si no se puede factorizar el polinomio por inspección, utiliza la fórmula general para encontrar las raíces del polinomio: x = (-b ± √(b^2 - 4ac)) / 2a. Si las raíces obtenidas son números racionales, entonces el polinomio se puede factorizar utilizando la fórmula: ax^2 + bx + c = a(x - r1)(x - r2), donde r1 y r2 son las raíces del polinomio. Para factorizar un polinomio cuadrático de la forma x^2 + bx + c, donde b y c son coeficientes numéricos, sigue los siguientes pasos: Busca dos números que sumados den como resultado b y multiplicados den como resultado c. Estos números serán los coeficientes de los términos lineales en la factorización. Escribe el polinomio original como la suma de dos términos, utilizando los números obtenidos en el paso anterior. Por ejemplo, si los números son r y s, entonces podemos escribir el polinomio como x^2 + bx + c = x^2 + rx + sx + c. Agrupa los primeros dos términos y los últimos dos términos en dos grupos separados. Factoriza el factor común de cada grupo. Factoriza el término común de ambos grupos. Reescribe la factorización en términos de la suma de los dos términos encontrados en el paso 2. Factorización por diferencia de cuadrados: Si el polinomio es de la forma "a² - b²", puede ser factorizado por diferencia de cuadrados utilizando la fórmula (a+b)(a-b) = a² - b². Factorización por suma y diferencia de cubos: Identifica el polinomio como una suma o diferencia de cubos. Un polinomio de la forma a^3 + b^3 es una suma de cubos, mientras que un polinomio de la forma a^3 - b^3 es una diferencia de cubos. Si el polinomio es una suma de cubos, factoriza el polinomio utilizando la siguiente fórmula: a^3 + b^3 = (a + b)(a^2 - ab + b^2) Si el polinomio es una diferencia de cubos, factoriza el polinomio utilizando la siguiente fórmula: a^3 - b^3 = (a - b)(a^2 + ab + b^2) Verifica que no se puedan factorizar más los términos en las expresiones obtenidas. Si los términos de las expresiones obtenidas son factores lineales irreducibles, entonces el polinomio original ha sido completamente factorizado. Factorización por método de Ruffini: Escribe el polinomio en orden descendente de exponentes. Por ejemplo, si el polinomio es 2x^3 - 3x^2 + 5x - 6, escríbelo como 2 -3 5 -6. Identifica el binomio del que deseas dividir el polinomio. En el método de Ruffini, este binomio siempre será de la forma (x - a), donde "a" es un número real. Por ejemplo, si deseas dividir el polinomio anterior por (x - 2), "a" sería 2. Escribe el número "a" en la primera fila de la tabla de Ruffini, debajo del coeficiente más alto del polinomio. En el ejemplo anterior, escribe 2 debajo del 2. Copia el primer coeficiente del polinomio en la segunda fila de la tabla de Ruffini, debajo del número "a". En este ejemplo, escribe 2 debajo de 2. Multiplica el número "a" por el coeficiente que acabas de copiar y escribe el resultado en la tercera fila. En este ejemplo, 2 x 2 = 4, por lo que escribe 4 debajo del -3. Suma los coeficientes de la segunda y tercera fila y escribe el resultado en la cuarta fila. En este ejemplo, -3 + 4 = 1, por lo que escribe 1 debajo del 5. Multiplica el número "a" por el coeficiente que acabas de copiar y escribe el resultado en la quinta fila. En este ejemplo, 2 x 1 = 2, por lo que escribe 2 debajo del -6. Suma los coeficientes de la cuarta y quinta fila y escribe el resultado en la sexta fila. En este ejemplo, 5 + 2 = 7, por lo que escribe 7 en la sexta fila. Lee el último número de la tabla. Este número es el residuo de la división. Si es igual a cero, significa que el binomio (x - a) es un factor del polinomio original. En este ejemplo, el residuo es 7, lo que significa que (x - 2) no es un factor del polinomio original. Si el residuo es igual a cero, los coeficientes de la primera fila (excluyendo el número "a") representan los coeficientes del polinomio factorizado. En este ejemplo, los coeficientes son 2, 1 y 7, por lo que el polinomio factorizado es 2x^2 + x + 7.

En el caso de no poder factorizar por estos métodos utilizar el método de evaluación:

Identificar el grado del polinomio: El grado del polinomio se refiere al exponente más alto en la expresión. Por ejemplo, en el polinomio 2x^3 - 3x^2 + 5x - 6, el grado es 3. Determinar los factores constantes: El término constante del polinomio es el término que no tiene una variable. En el ejemplo anterior, el término constante es -6. Los factores constantes son los factores de este término. En este caso, los factores de -6 son -1, 1, -2, 2, -3, 3 y -6, 6. Evaluar el polinomio en cada factor constante: Sustituya cada uno de los factores constantes en lugar de "x" en el polinomio y evalúe el resultado. Por ejemplo, para el factor -1, el polinomio se convierte en 2(-1)^3 - 3(-1)^2 + 5(-1) - 6, lo que da como resultado -2. Realice esta evaluación para cada uno de los factores constantes. Identificar los factores comunes: Si hay factores comunes en las evaluaciones, éstos pueden ser factorizados. Por ejemplo, en las evaluaciones del polinomio anterior, -2 y 0 son comunes en los resultados, lo que indica que el polinomio tiene un factor común de (x + 2) y x. Dividir el polinomio por el factor común: Divida el polinomio por el factor común identificado en el paso anterior. En el ejemplo anterior, dividir el polinomio por (x + 2) y x. Esto da como resultado el polinomio factorizado completo. Verificar los resultados: Una vez que se ha realizado la factorización, es importante verificar que el resultado es correcto. Para hacer esto, multiplique los factores y verifique que el resultado sea igual al polinomio original. Verificar los resultados: Una vez que se han realizado los pasos anteriores, es importante verificar que la factorización es correcta. Para hacer esto, multiplique los factores y verifique que el resultado sea igual al polinomio original.